Browsed by
Month: October 2019

The Dartboard Paradox

The Dartboard Paradox

On November 5, 2019, I will be at PyData NYC to give a talk called The Inspection Paradox is Everywhere [UPDATE: The video from the talk is here]. Here’s the abstract:

The inspection paradox is a statistical illusion you’ve probably never heard of. It’s a common source of confusion, an occasional cause of error, and an opportunity for clever experimental design. And once you know about it, you see it everywhere.

The examples in the talk include social networks, transportation, education, incarceration, and more. And now I am happy to report that I’ve stumbled on yet another example, courtesy of John D. Cook.

In a blog post from 2011, John wrote about the following counter-intuitive truth:

For a multivariate normal distribution in high dimensions, nearly all the probability mass is concentrated in a thin shell some distance away from the origin.

John does a nice job of explaining this result, so you should read his article, too. But I’ll try to explain it another way, using a dartboard.

If you are not familiar with the layout of a “clock” dartboard, it looks like this:

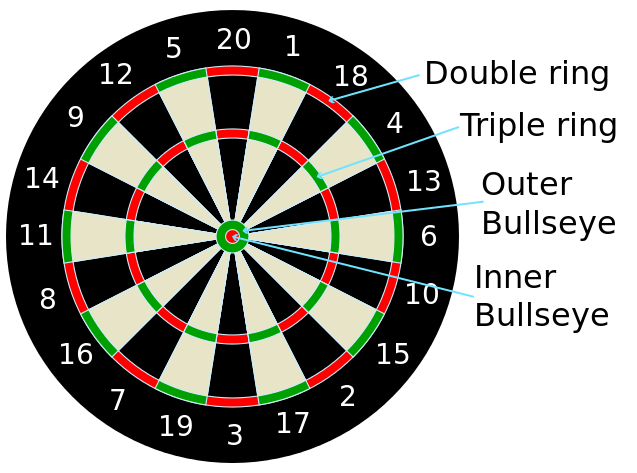
File:Dartboard diagram.svg

I got the measurements of the board from the British Darts Organization rules, and drew the following figure with dimensions in mm:

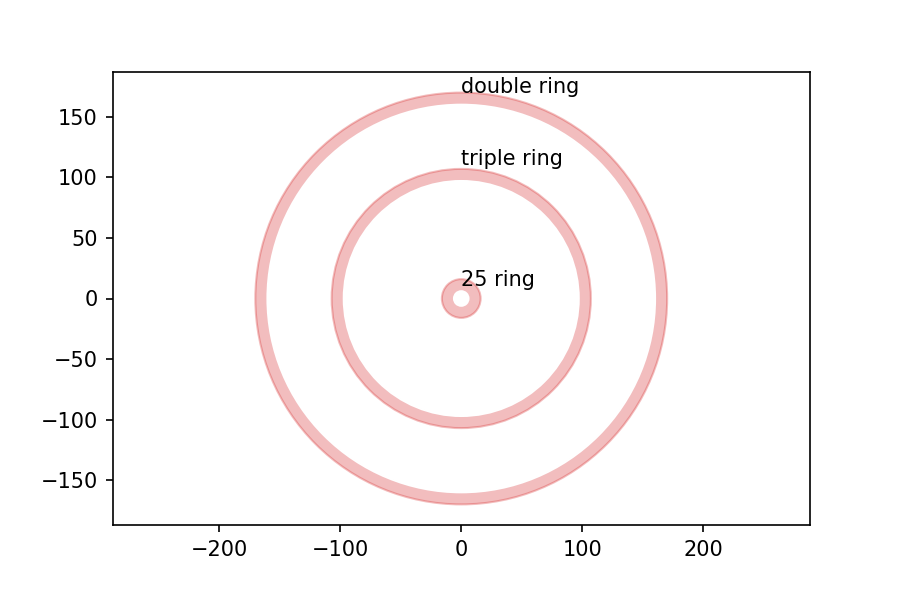
Now, suppose I throw 100 darts at the board, aiming for the center each time, and plot the location of each dart. It might look like this:

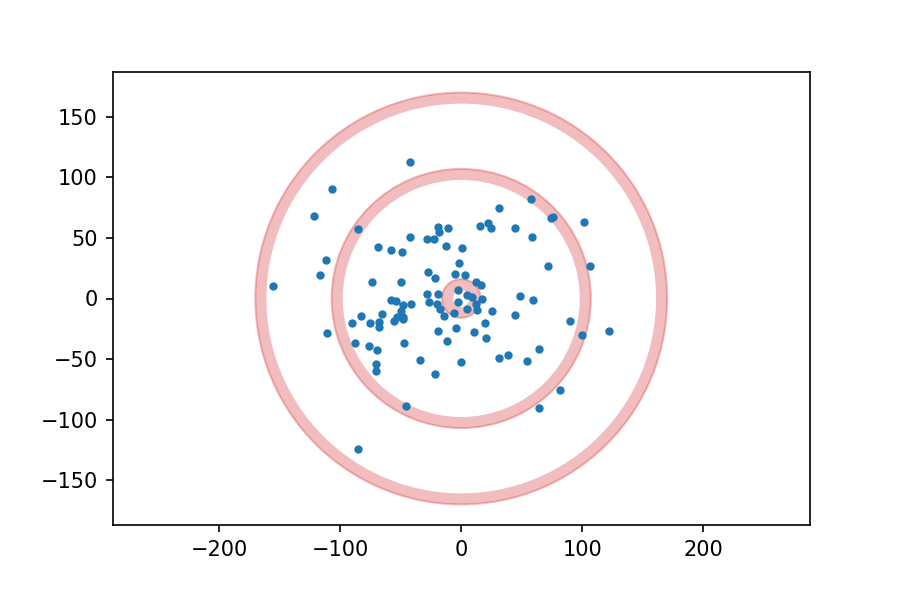
Suppose we analyze the results and conclude that my errors in the x and y directions are independent and distributed normally with mean 0 and standard deviation 50 mm.

Assuming that model is correct, then, which do you think is more likely on my next throw, hitting the 25 ring (the innermost red circle), or the triple ring (the middlest red circle)?

It might be tempting to say that the 25 ring is more likely, because the probability density is highest at the center of the board and lower at the triple ring.

We can see that by generating a large sample, generating a 2-D kernel density estimate (KDE), and plotting the result as a contour.

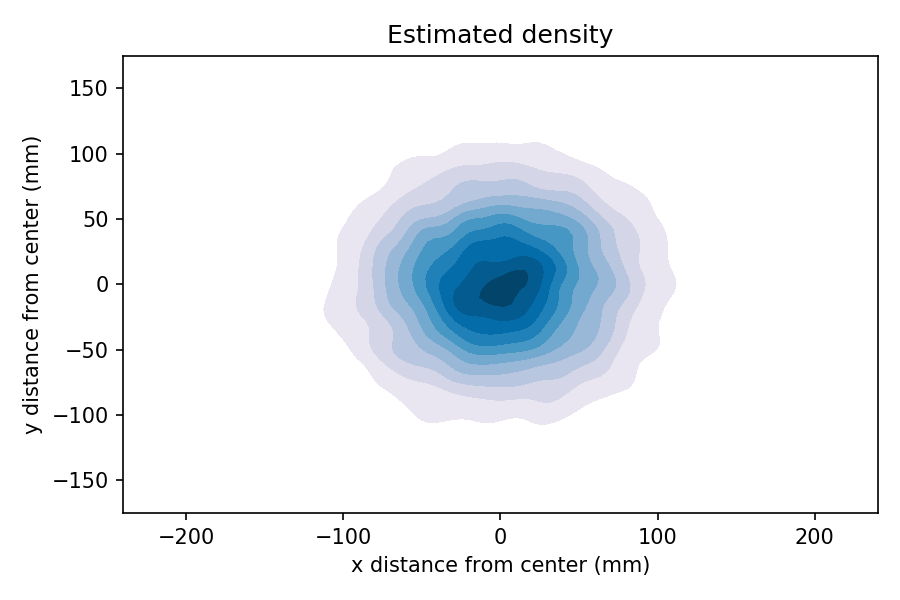
In the contour plot, darker color indicates higher probability density. So it sure looks like the inner ring is more likely than the outer rings.

But that’s not right, because we have not taken into account the area of the rings. The total probability mass in each ring is the product of density and area (or more precisely, the density integrated over the area).

The 25 ring is more dense, but smaller; the triple ring is less dense, but bigger. So which one wins?

In this example, I cooked the numbers so the triple ring wins: the chance of hitting triple ring is about 6%; the chance of hitting the double ring is about 4%.

If I were a better dart player, my standard deviation would be smaller and the 25 ring would be more likely. And if I were even worse, the double ring (the outermost red ring) might be the most likely.

Inspection Paradox?

It might not be obvious that this is an example of the inspection paradox, but you can think of it that way. The defining characteristic of the inspection paradox is length-biased sampling, which means that each member of a population is sampled in proportion to its size, duration, or similar quantity.

In the dartboard example, as we move away from the center, the area of each ring increases in proportion to its radius (at least approximately). So the probability mass of a ring at radius r is proportional to the density at r, weighted by r.

We can see the effect of this weighting in the following figure:

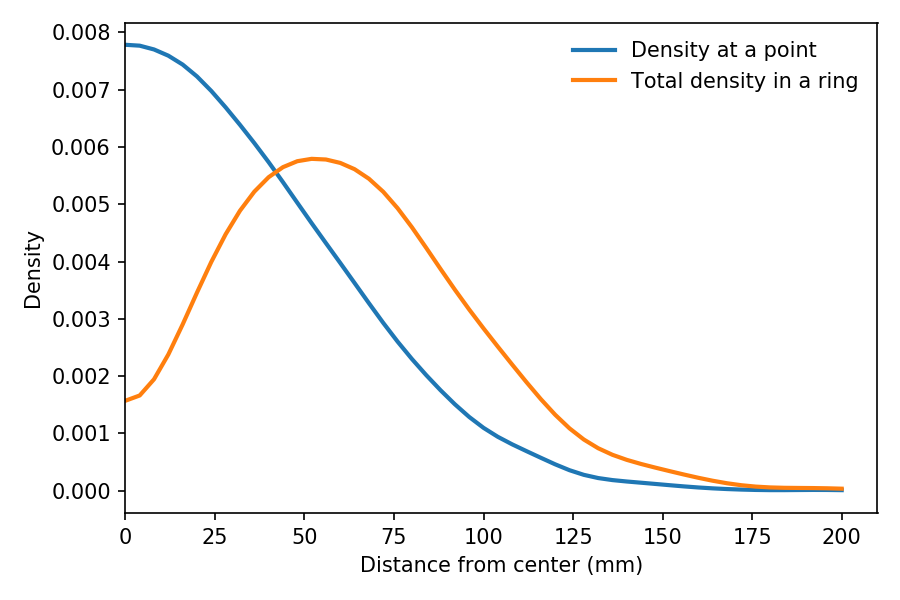
The blue line shows estimated density as a function of r, based on a sample of throws. As expected, it is highest at the center, and drops away like one half of a bell curve.

The orange line shows the estimated density of the same sample weighted by r, which is proportional to the probability of hitting a ring at radius r.

It peaks at about 60 mm. And the total density in the triple ring, which is near 100 mm, is a little higher than in the 25 ring, near 10 mm.

If I get a chance, I will add the dartboard problem to my talk as yet another example of length-biased sampling, also known as the inspection paradox.

You can see my code for this example in this Jupyter notebook.

UPDATE November 6, 2019: This “thin shell” effect has practical consequences. This excerpt from The End of Average talks about designing the cockpit of a plan for the “average” pilot, and discovering that there are no pilots near the average in 10 dimensions.

What should you do?

What should you do?

In my previous post I asked “What should I do?“. Now I want to share a letter I wrote recently for students at Olin, which appeared in our school newspaper, Frankly Speaking.

It is addressed to engineering students, but it might also be relevant to people who are not students or not engineers.

Dear Students,

As engineers, you have a greater ability to affect the future of the planet than almost anyone else.  In particular, the decisions you make as you start your careers will have a disproportionate impact on what the world is like in 2100.

Here are the things you should work on for the next 80 years that I think will make the biggest difference:

  • Nuclear energy
  • Desalination
  • Transportation without fossil fuels
  • CO₂ sequestration
  • Alternatives to meat
  • Global education
  • Global child welfare
  • Infrastructure for migration
  • Geoengineering

Let me explain where that list comes from.

First and most importantly, we need carbon-free energy, a lot of it, and soon.  With abundant energy, almost every other problem is solvable, including food and desalinated water.  Without it, almost every other problem is impossible.

Solar, wind, and hydropower will help, but nuclear energy is the only technology that can scale up enough, soon enough, to substantially reduce carbon emissions while meeting growing global demand.

With large scale deployment of nuclear power, it is feasible for global electricity production to be carbon neutral by 2050 or sooner.  And most energy use, including heat, agriculture, industry, and transportation, could be electrified by that time. Long-range shipping and air transport will probably still require fossil fuels, which is why we also need to develop carbon capture and sequestration.

Global production of meat is a major consumer of energy, food, and water, and a major emitter of greenhouse gasses.  Developing alternatives to meat can have a huge impact on climate, especially if they are widely available before meat consumption increases in large developing countries.

World population is expected to peak in 2100 at 9 to 11 billion people.  If the peak is closer to 9 than 11, all of our problems will be 20% easier.  Fortunately, there are things we can do to help that happen, and even more fortunately, they are good things.

The difference between 9 and 11 depends mostly on what happens in Africa during the next 30 years.  Most of the rest of the world has already made the “demographic transition“, that is, the transition from high fertility (5 or more children per woman) to low fertility (at or below replacement rate).

The primary factor that drives the demographic transition is child welfare; increasing childhood survival leads to lower fertility.  So it happens that the best way to limit global population is to protect children from malnutrition, disease, and violence. Other factors that contribute to lower fertility are education and economic opportunity, especially for women.

Regardless of what we do in the next 50 years, we will have to deal with the effects of climate change, and a substantial part of that work will be good old fashioned civil engineering.  In particular, we need infrastructure like sea walls to protect people and property from natural disasters. And we need a new infrastructure of migration, including the ability to relocate large numbers of people in the short term, after an emergency, and in the long term, when current population centers are no longer viable.

Finally, and maybe most controversially, I think we will need geoengineering.  This is a terrible and dangerous idea for a lot of reasons, but I think it is unavoidable, not least because many countries will have the capability to act unilaterally.  It is wise to start experiments now to learn as much as we can, as long as possible before any single actor takes the initiative.

Think locally, act globally

When we think about climate change, we gravitate to individual behavior and political activism.  These activities are appealing because they provide opportunities for immediate action and a feeling of control.  But they are not the best tools you have.

Reducing your carbon footprint is a great idea, but if that’s all you do, it will have a negligible effect.

And political activism is great: you should vote, make sure your representatives know what you think, and take to the streets if you have to.  But these activities have diminishing returns. Writing 100 letters to your representative is not much better than one, and you can’t be on strike all the time.

If you focus on activism and your personal footprint, you are neglecting what I think is your greatest tool for impact: choosing how you spend 40 hours a week for the next 80 years of your life.

As an early-career engineer, you have more ability than almost anyone else to change the world.  If you use that power well, you will help us get through the 21st Century with a habitable planet and a high quality of life for the people on it.