Browsed by
Month: October 2020

Millennials are not getting married

Millennials are not getting married

In 2015 I wrote a paper called “Will Millennials Ever Get Married?” where I used data from the National Survey of Family Growth (NSFG) to estimate the age at first marriage for women in the U.S, broken down by decade of birth.  

I found that women born in the 1980s and 90s were getting married later than previous cohorts, and I generated projections that suggest they are on track to stay unmarried at substantially higher rates.

Here are the results from that paper, based on 58 488 women surveyed between 1983 to 2015:

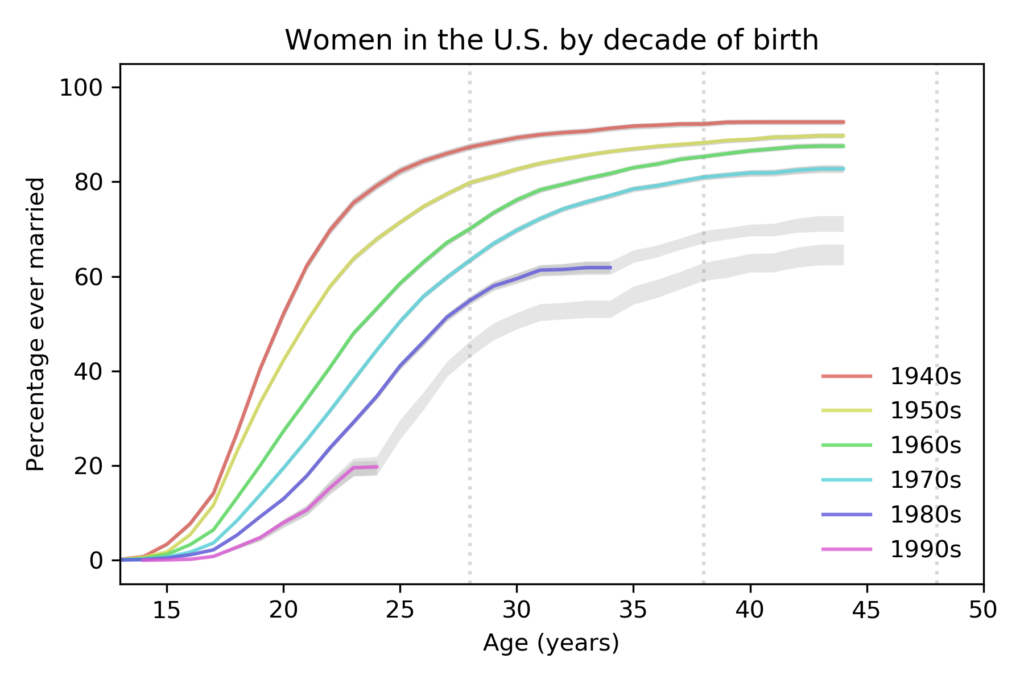
Percentage of women ever married, based on data up to 2015.

Each line represents a cohort grouped by decade of birth. For example, the top line represents women born in the 1940s.

The colored segments show the fraction of women who had ever been married as a function of age. For example, among women born in the 1940s, 82% had been married by age 25. Among women born in the 1980s, only 41% had been married by the same age.

The gray lines show projections I generated by assuming that going forward each cohort would be subject to the hazard function of the previous cohort. This method is likely to overestimate marriage rates.

These results show two trends:

  • Each cohort is getting married later than the previous cohort.
  • The fraction of women who never marry is increasing from one cohort to the next.

New data

Yesterday the National Center for Health Statistics (NCHS) released a new batch of data from surveys conducted in 2017-2019.  So we can compare the predictions from 2015 with the new data, and generate updated predictions.

The following figure shows the predictions from the previous figure, which are based on data up to 2015, compared to the new curves based on data up to 2019, which includes 70 183 respondents.

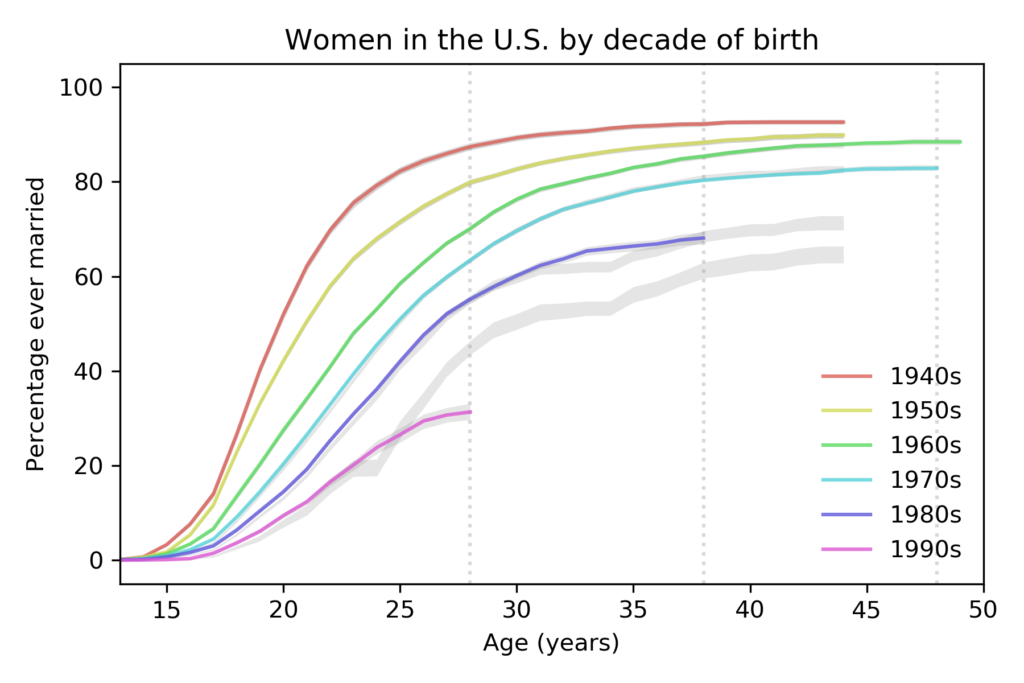
Percentage of women ever married, based on data up to 2019,
compared to predictions based on data up to 2015.

For women born in the 1980s, the fraction who have married is almost exactly as predicted. For women born in the 1990s, it is substantially lower.

New projections

The following figure shows projections based on data up to 2019.

Percentage of women ever married, based on data up to 2019,
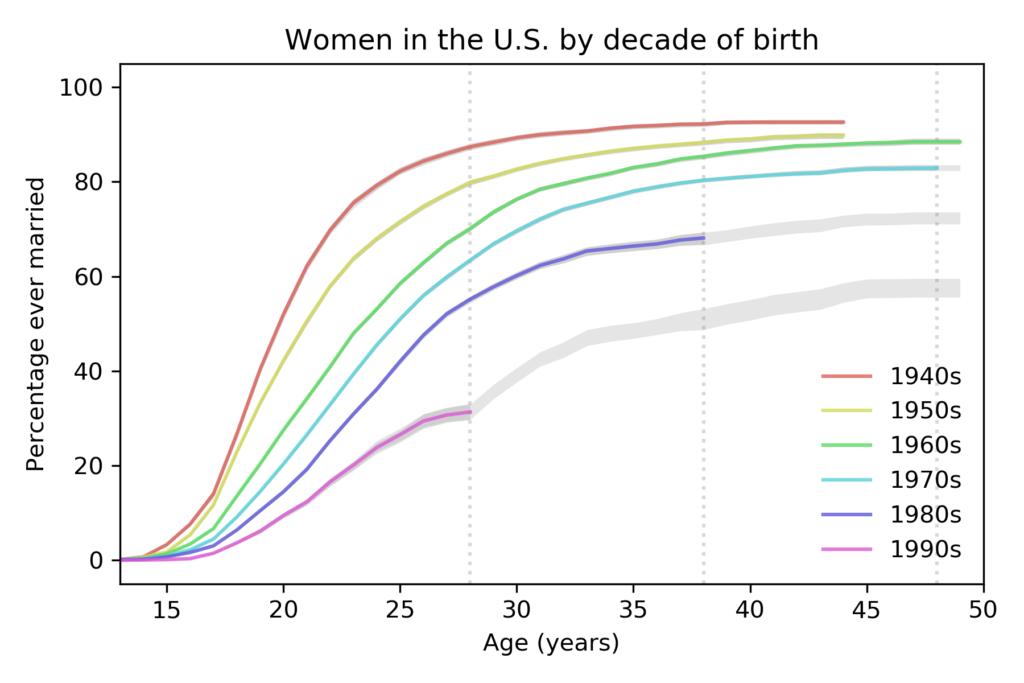
with predictions based on data up to 2019.

The vertical dashed lines show the ages where we have the last reliable estimate for each cohort. The following table summarizes the results at age 28:

Decade of birth1940s1950s1960s1970s1980s1990s
% married
before age 28		87%80%70%63%55%31%
Percentage of women married by age 28, grouped by decade of birth.

The percentage of women married by age 28 has dropped quickly from each cohort to the next, by about 11 percentage points per decade.

The following table shows the same percentage at age 38; the last value, for women born in the 1990s, is a projection based on the data we have so far.

Decade of birth1940s1950s1960s1970s1980s1990s
% married
before age 38		92%88%85%80%68%51%
Percentage of women married by age 38, grouped by decade of birth.

Based on current trends, we expect barely half of women born in the 1990s to be married before age 38.

Finally, here are the percentages of women married by age 48; the last two values are projections.

Decade of birth1940s1950s1960s1970s1980s1990s
% married
before age 48		>93%>90%88%83%72%58%
Percentage of women married by age 48, grouped by decade of birth.

Based on current trends, we expect women born in the 1980s and 1990s to remain unmarried at rates substantially higher than previous generations.

Projections like these are based on the assumption that the future will be like the past, but of course, things change. In particular:

  • These data were collected before the COVID-19 pandemic. Marriage rates in 2020 will probably be lower than predicted, and the effect could continue into 2021 or beyond.
  • However, as economic conditions improve in the future, marriage rates might increase.

We’ll find out when we get the next batch of data in October 2022.

The code I used for this analysis is in this GitHub repository.

Whatever the question was, correlation is not the answer

Whatever the question was, correlation is not the answer

Pearson’s coefficient of correlation, r, is one of the most widely-reported statistics. But in my opinion, it is useless; there is no good reason to report it, ever.

Most of the time, what you really care about is either effect size or predictive value:

  • To quantify effect size, report the slope of a regression line.

If there’s no reason to prefer one measure over another, report reduction in RMSE, because you can compute it directly from R².

If you don’t care about effect size or predictive value, and you just want to show that there’s a (linear) relationship between two variables, use R², which is more interpretable than r, and exaggerates the strength of the relationship less.

In summary, there is no case where r is the best statistic to report. Most of the time, it answers the wrong question and makes the relationship sound more important than it is.

To explain that second point, let me show an example.

Height and weight

I’ll use data from the BRFSS to quantify the relationship between weight and height. Here’s a scatter plot of the data and a regression line:

The slope of the regression line is 0.9 kg / cm, which means that if someone is 1 cm taller, we expect them to be 0.9 kg heavier. If we care about effect size, that’s what we should report.

If we care about predictive value, we should compare predictive error with and without the explanatory variable.

  • Without the model, the estimate that minimizes mean absolute error (MAE) is the median; in that case, the MAE is about 15.9 kg.
  • With the model, MAE is 13.8 kg.

So the model reduces MAE by about 13%.

If you don’t care about effect size or predictive value, you are probably up to no good. But even in that case, you should report R² = 0.22 rather than r = 0.47, because

  • R² can be interpreted as the fraction of variance explained by the model; I don’t love this interpretation because I think the use of “explained” is misleading, but it’s better than r, which has no natural interpretation.
  • R² is generally smaller than r, which means it exaggerates the strength of the relationship less.

[UPDATE: Katie Corker corrected my claim that r has no natural interpretation: it is the standardized slope. In this example, we expect someone who is one standard deviation taller than the mean to be 0.47 standard deviations heavier than the mean. Sebastian Raschka does a nice job explaining this here.]

In general…

This dataset is not unusual. R² and r generally overstate the predictive value of the model.

The following figure shows the relationship between r, R², and the reduction in RMSE.

Values of r that sound impressive correspond to values of R² that are more modest and to reductions in RMSE which are substantially less impressive.

This inflation is particularly hazardous when r is small. For example, if you see r = 0.25, you might think you’ve found an important relationship. But that only “explains” 6% of the variance, and in terms of predictive value, only decreases RMSE by 3%.

In some contexts, that predictive value might be useful, but it is substantially more modest than r=0.25 might lead you to believe.

The details of this example are in this Jupyter notebook.

And the analysis I used to generate the last figure is in this notebook.