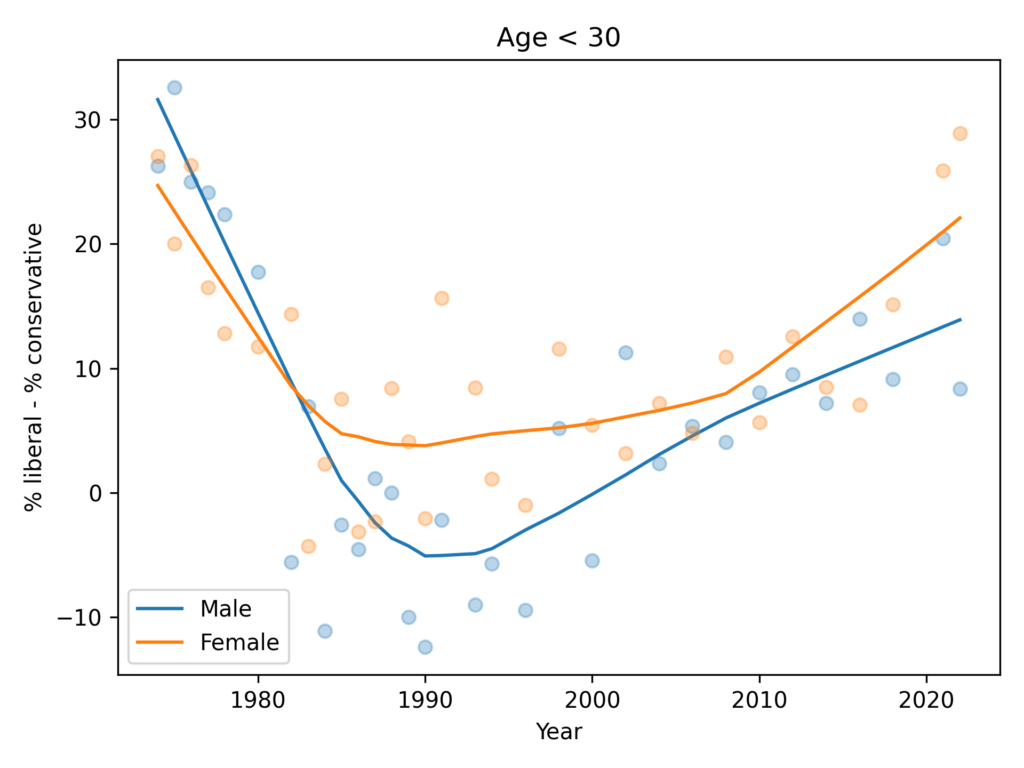
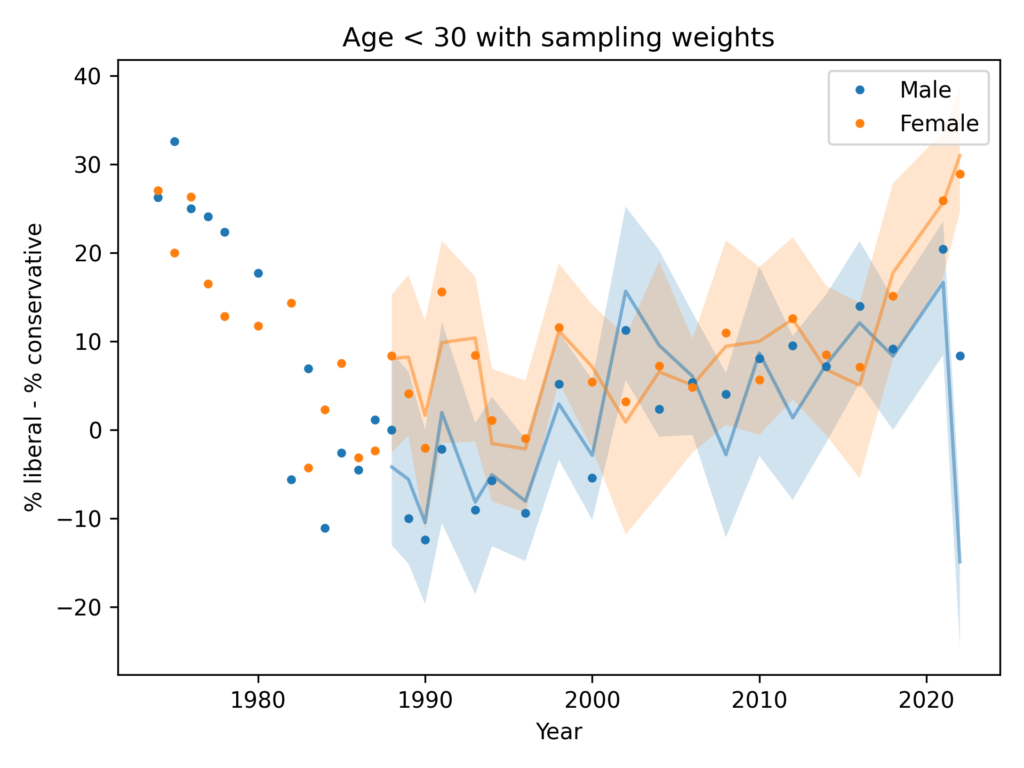
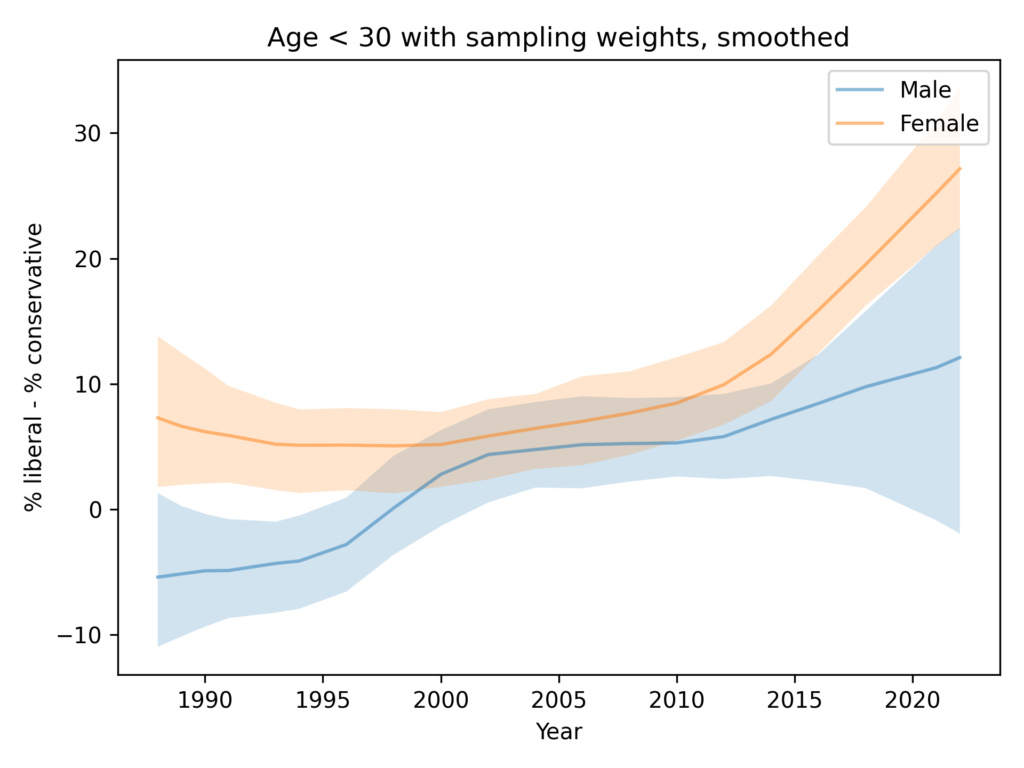
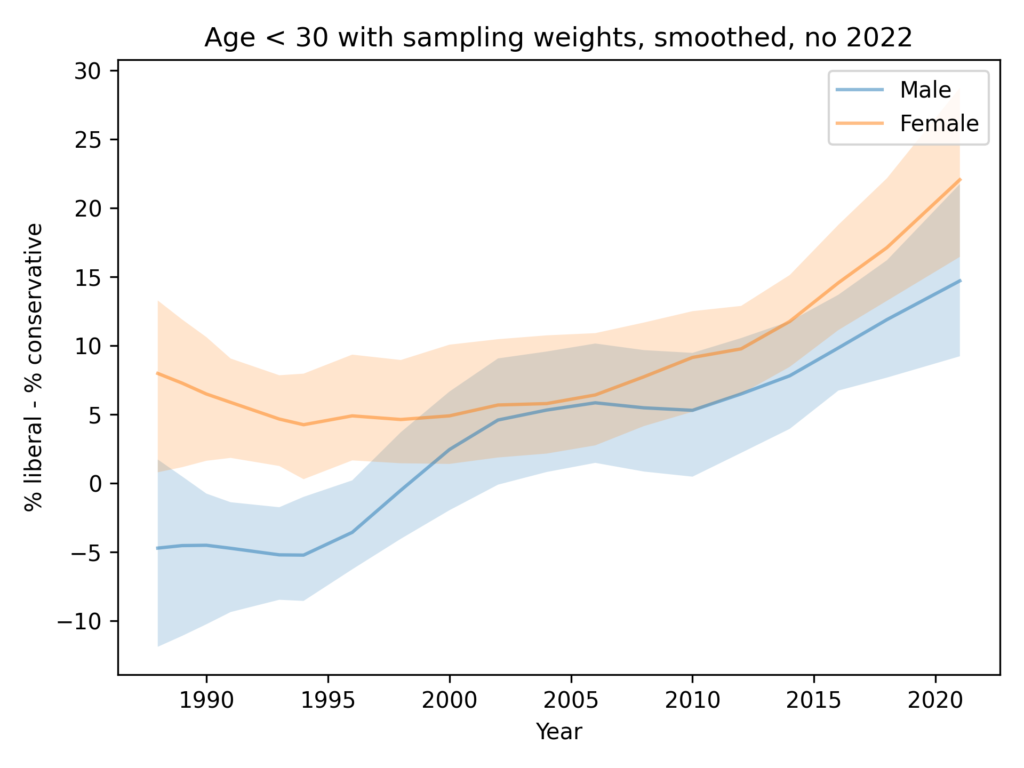
What does a confidence interval mean?
Here’s another installment in Data Q&A: Answering the real questions with Python. In general, I will try to focus on practical problems, but this one is a little more philosophical.
What does a confidence interval mean?¶
Here’s a question from the Reddit statistics forum (with an edit for clarity):
Why does a confidence interval not tell you that 90% of the time, [the true value of the population parameter] will be in the interval, or something along those lines?
I understand that the interpretation of confidence intervals is that with repeated samples from the population, 90% of the time the interval would contain the true value of whatever it is you’re estimating. What I don’t understand is why this method doesn’t really tell you anything about what that parameter value is.
This is, to put it mildly, a common source of confusion. And here is one of the responses:
From a frequentist perspective, the true value of the parameter is fixed. Thus, once you have calculated your confidence interval, one if two things are true: either the true parameter value is inside the interval, or it is outside it. So the probability that the interval contains the true value is either 0 or 1, but you can never know which.
This response is the conventional answer to this question — it is what you find in most textbooks and what is taught in most classes. And, in my opinion, it is wrong. To explain why, I’ll start with a story.
Suppose Frank and Betsy visit a factory where 90% of the widgets are good and 10% are defective. Frank chooses a part at random and asks Betsy, “What is the probability that this part is good?”
Betsy says, “If 90% of the parts are good, and you choose one at random, the probability is 90% that it is good.”
“Wrong!” says Frank. “Since the part has already been manufactured, one of two things must be true: either it is good or it is defective. So the probability is either 100% or 0%, but we don’t know which.”
Frank’s argument is based on a strict interpretation of frequentism, which is a particular philosophy of probability. But it is not the only interpretation, and it is not a particularly good one. In fact, it suffers from several flaws. This example shows one of them — in many real-world scenarios where it would be meaningful and useful to assign a probability to a proposition, frequentism simply refuses to do so.
Fortunately, Betsy is under no obligation to adopt Frank’s interpretation of probability. She is free to adopt any of several alternatives that are consistent with her commonsense claim that a randomly-chosen part has a 90% probability of being functional.
Now let’s see how this story relates to confidence intervals.
I’ll start by importing the usual libraries.
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
Generating a confidence interval¶
Suppose that Frank is a statistics teacher and Betsy is one of his students. One day Frank teaches the class a process for computing confidence intervals that goes like this:
Collect a sample of size $n$.
Compute the sample mean, $m$, and the sample standard deviation, $s$.
If those estimates are correct, the sampling distribution of the mean is a normal distribution with mean $m$ and standard deviation $s / \sqrt{n}$.
Compute the 5th and 95th percentiles of this sampling distribution. The result is a 90% confidence interval.
As an example, Frank generates a sample with size 100 from a normal distribution with known parameters mean $\mu=10$ and standard deviation $\sigma=3$.
from scipy.stats import norm
mu = 10
sigma = 3
np.random.seed(17)
data = norm.rvs(mu, sigma, size=100)
Then Betsy uses the following function to compute a 90% CI.
def compute_ci(data):
n = len(data)
m = np.mean(data)
s = np.std(data)
sampling_dist = norm(m, s / np.sqrt(n))
ci90 = sampling_dist.ppf([0.05, 0.95])
return ci90
ci90 = compute_ci(data)
ci90
array([ 9.78147291, 10.88758585])
In this example, we know that the actual population mean is 10 so we can see that this CI contains the population mean. But if we draw another sample, we might get a sample mean that is substantially higher or lower than $\mu$, and the CI we compute might not contain $\mu$.
To see how often that happens, we’ll use this function, which generates a sample, computes a 90% CI, and checks whether the CI contains $\mu$.
def run_experiment(mu, sigma):
data = norm.rvs(mu, sigma, size=100)
low, high = compute_ci(data)
return low < mu < high
If we run this function 1000 times, we can count how often the CI contains $\mu$.
np.mean([run_experiment(mu, sigma) for i in range(1000)]) * 100
90.60000000000001
The answer is close to 90% — that is, if we run this process many times, 90% of the CIs it generates contain $\mu$ and 10% don’t. So the CI-computing process is like a factory where 90% of the widgets are good and 10% are defective.
Now suppose Frank chooses a different value of $\mu$ and does not tell Betsy what it is. To simulate that scenario, I’ll choose a value from a random number generator with a specific seed.
np.random.seed(17)
unknown_mu = np.random.uniform(10, 20)
And just for good measure, I’ll generate a random value for $\sigma$, too.
unknown_sigma = np.random.uniform(2, 3)
Next Frank generates a sample from a normal distribution with those parameters, and gives the sample to Betsy.
data2 = norm.rvs(unknown_mu, unknown_sigma, size=100)
And Betsy uses the data to compute a CI.
compute_ci(data2)
array([12.81278165, 13.73152148])
Now suppose Frank asks, “What is the probability that this CI contains the actual value of $\mu$ that I chose?”
Betsy says, “We have established that 90% of the CIs generated by this process contain $\mu$, so the probability that this CI contains $\mu$ is 90%.”
And of course Frank says “Wrong! Now that we have computed the CI, it is unknown whether it contains the true parameter, but it is not random. The probability that it contains $\mu$ is either 100% or 0%. We can’t say it has a 90% chance of containing $\mu$.”
Once again, Frank is asserting a particular interpretation of probability — one that has the regrettable property of rendering probability nearly useless. Fortunately, Betsy is under no obligation to join Frank’s cult.
Under most reasonable interpretations of probability, you can say that a specific 90% CI has a 90% chance of containing the true parameter. There is no real philosophical problem with that.
But there might be practical problems.
Practical problems¶
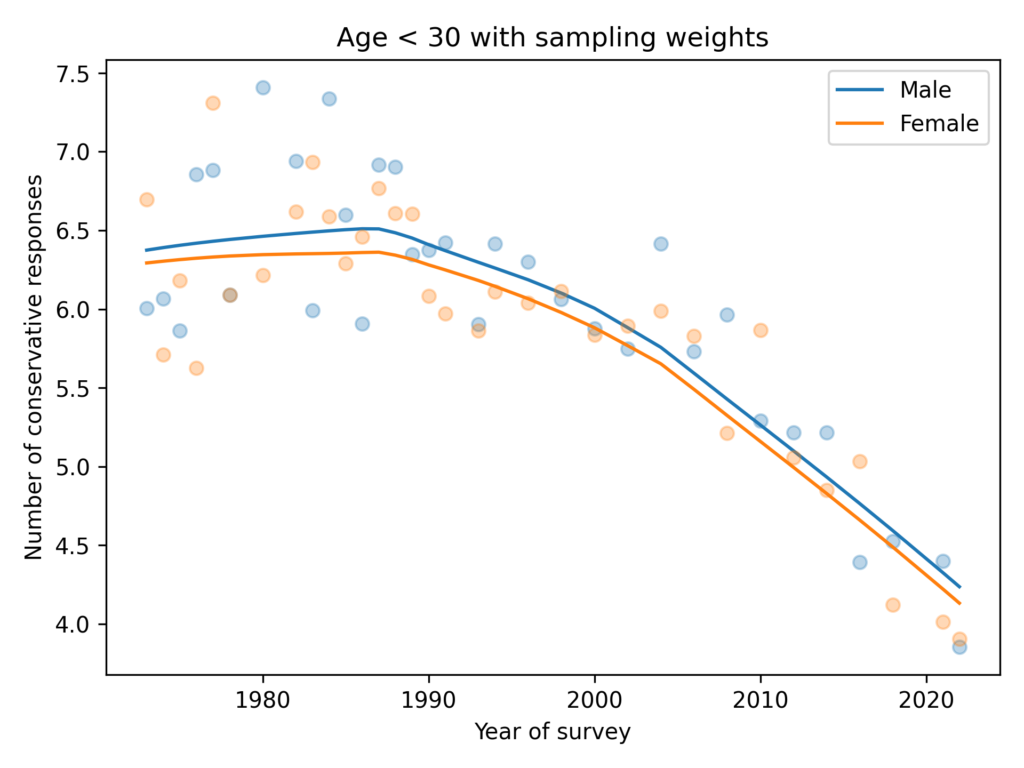
The process we use to construct a CI takes into account variability due to random sampling, but it does not take into account other problems, like measurement error and non-representative sampling. To see why that matters, let’s consider a more realistic example.
Suppose we want to estimate the average height of adult male residents of the United States. If we define terms like “height”, “adult”, “male”, and “resident of the United States” precisely enough, we have defined a population that has a true, unknown average height. If we collect a representative sample from the population and measure their heights, we can use the sample mean to estimate the population mean and compute a confidence interval.
To demonstrate, I’ll use data from the Behavioral Risk Factor Surveillance System (BRFSS). Here’s an extract I prepared for Elements of Data Science, based on BRFSS data from 2021.
from os.path import basename, exists
def download(url):
filename = basename(url)
if not exists(filename):
from urllib.request import urlretrieve
local, _ = urlretrieve(url, filename)
print("Downloaded " + str(local))
return filename
download('https://github.com/AllenDowney/ElementsOfDataScience/raw/v1/data/brfss_2021.hdf')
'brfss_2021.hdf'
brfss = pd.read_hdf('brfss_2021.hdf', 'brfss')
It includes data from 203,760 male respondents.
male = brfss.query('_SEX == 1')
len(male)
203760
For 193,701 of them, we have their self-reported height recorded in centimeters.
male['HTM4'].count()
193701
We can use this data to compute a sample mean and 90% confidence interval.
m = male['HTM4'].mean()
ci90 = compute_ci(male['HTM4'])
m, ci90
(178.14807357731763, array([178.11896943, 178.17717773]))
Because the sample size is so large, the confidence interval is quite small — its width is only 0.03% of the estimate.
np.diff(ci90) / m * 100
array([0.03267411])
So there is very little variability in this estimate due to random sampling. That means the estimate is precise, but that doesn’t mean it’s accurate.
For one thing, the measurements in this dataset are self-reported. If people tend to round up — and they do — that would make the estimated mean too high.
For another thing, it is difficult to construct a representative sample of a population as large as the United States. The BRFSS is run by people who know what they are doing, but nothing is perfect — it is likely that some groups are systematically overrepresented or underrepresented. And that could make the estimated mean too high or too low.
Given that there is almost certainly some measurement error and some sampling bias, it is unlikely that the actual population falls in the very small confidence interval we computed.
And that’s true in general — when the sample size is large, variability due to random sampling is small, which means that other sources of error are likely to be bigger. So as sample size increases, the probability decreases that the CI contains the true value.
Summary¶
The way confidence intervals are taught in most statistics class is based on the frequentist interpretation of probability. But you are not obligated to adopt that interpretation, and there are good reasons you should not.
Some people will say that confidence intervals are a frequentist method that is inextricable from the frequentist interpretation. I don’t think that’s true — there is nothing about the computation of a confidence interval that depends on the frequentist interpretation. So you are free to interpret the CI under any philosophy of probability you like.
If you want to say that a 90% CI has a 90% chance of containing the true value, there is nothing wrong with that, philosophically. I think it is a meaningful and useful probabilistic claim.
However, it is only true if other sources of error — like sampling bias and measurement error — are small compared to variability due to random sampling.
For that reason, I think the best interpretation of a confidence interval, for practical purposes, is that it quantifies the precision of the estimate but says nothing about its accuracy.
Credit: I borrowed Frank and Betsy from my friend Ted Bunn. They first appeared in his blog post Who knows what evil lurks in the hearts of men? The Bayesian doesn’t care..