Whatever the question was, correlation is not the answer
Pearson’s coefficient of correlation, r, is one of the most widely-reported statistics. But in my opinion, it is useless; there is no good reason to report it, ever.
Most of the time, what you really care about is either effect size or predictive value:
- To quantify effect size, report the slope of a regression line.
- To quantify predictive value, report a measure of predictive error that makes sense in context: MAE, MAPE, RMSE, whatever.
If there’s no reason to prefer one measure over another, report reduction in RMSE, because you can compute it directly from R².
If you don’t care about effect size or predictive value, and you just want to show that there’s a (linear) relationship between two variables, use R², which is more interpretable than r, and exaggerates the strength of the relationship less.
In summary, there is no case where r is the best statistic to report. Most of the time, it answers the wrong question and makes the relationship sound more important than it is.
To explain that second point, let me show an example.
Height and weight
I’ll use data from the BRFSS to quantify the relationship between weight and height. Here’s a scatter plot of the data and a regression line:
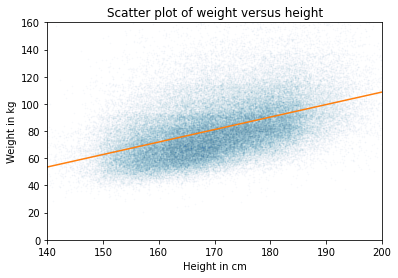
The slope of the regression line is 0.9 kg / cm, which means that if someone is 1 cm taller, we expect them to be 0.9 kg heavier. If we care about effect size, that’s what we should report.
If we care about predictive value, we should compare predictive error with and without the explanatory variable.
- Without the model, the estimate that minimizes mean absolute error (MAE) is the median; in that case, the MAE is about 15.9 kg.
- With the model, MAE is 13.8 kg.
So the model reduces MAE by about 13%.
If you don’t care about effect size or predictive value, you are probably up to no good. But even in that case, you should report R² = 0.22 rather than r = 0.47, because
- R² can be interpreted as the fraction of variance explained by the model; I don’t love this interpretation because I think the use of “explained” is misleading, but it’s better than r, which has no natural interpretation.
- R² is generally smaller than r, which means it exaggerates the strength of the relationship less.
[UPDATE: Katie Corker corrected my claim that r has no natural interpretation: it is the standardized slope. In this example, we expect someone who is one standard deviation taller than the mean to be 0.47 standard deviations heavier than the mean. Sebastian Raschka does a nice job explaining this here.]
In general…
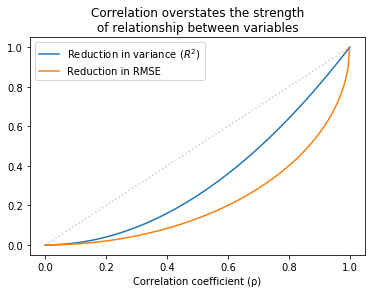
This dataset is not unusual. R² and r generally overstate the predictive value of the model.
The following figure shows the relationship between r, R², and the reduction in RMSE.
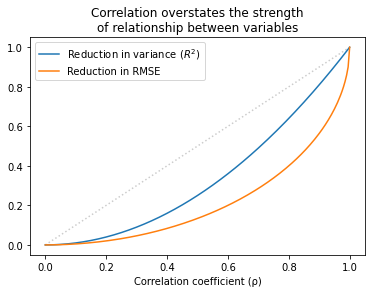
Values of r that sound impressive correspond to values of R² that are more modest and to reductions in RMSE which are substantially less impressive.
This inflation is particularly hazardous when r is small. For example, if you see r = 0.25, you might think you’ve found an important relationship. But that only “explains” 6% of the variance, and in terms of predictive value, only decreases RMSE by 3%.
In some contexts, that predictive value might be useful, but it is substantially more modest than r=0.25 might lead you to believe.
The details of this example are in this Jupyter notebook.
And the analysis I used to generate the last figure is in this notebook.