The following are abstracts from 13 projects where students in my Data Science class explore public data sets related to a variety of topics. Each abstract ends with a link to a report where you can see the details.
A Deeper Dive into US Suicides
Diego Berny and Anna Griffin
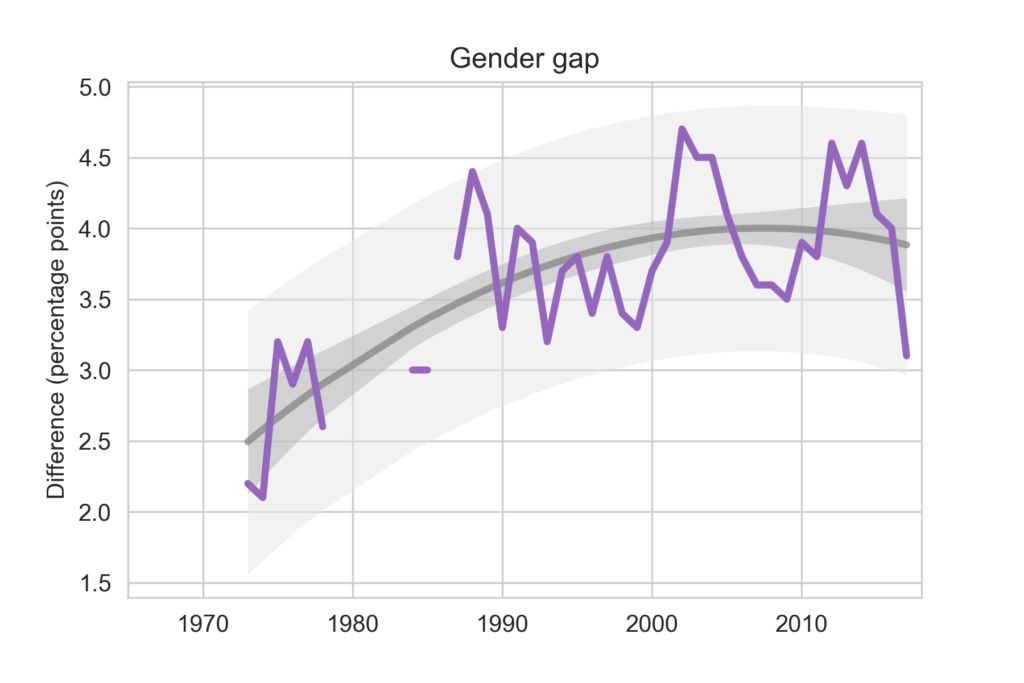
The world’s suicide rate has been decreasing over the past decade but unfortunately the United States’ rate is doing the exact opposite. Using data from the CDC and Our World in Data organizations, we explored different demographics to see if there are any patterns of vulnerable populations. We found that the group at the most risk is middle aged men. Men’s suicide rate is nearly 4 times higher than women’s and the group of adults between the ages of 45 and 59 has seen 36.5% increase over the past 17 years. When comparing their methods of suicide to their female counterparts we found that men tend to use more lethal means, resulting is less nonfatal suicide attempts. Read more
The Opioid Epidemic and Its Socioeconomic Effects
Daniel Connolly and Bryce Mann
Between 2002 and 2016, heroin use increased by 40%, while the use of other seemingly similar drugs declined in the same period. Using data from the National Survey on Drug Use and Health, we explore how the characteristics of opioid users have changed since the beginning of the epidemic. We find that so-called “late-starters” make up a new population of opioid users, as the average starting age of heroin users has increased by 2.5 years since 2002. We find a major discrepancy between the household incomes of users and nonusers as well, a discovery possibly related to socioeconomic factors like marriage. Read more
What is the Mother Tongue in U.S. Communities?
Allison Busa and Jordan Crawford-O’Banner
By watching the news, a person can assume that diversity is increasing rapidly in the United States. The current generation has been heralded as the most diverse in the history of the country. However, some Americans do not feel very positively about this change, and some even feel that the change is happening too rapidly. We decided to use the data from the U.S. Census to put these claims to the test. Using linguistic Census data, we ask “Is cultural diversity changing over time?” and “How is it spread out?” With PMFs, we analyze the number of people who speak a language other than English at home (SONELAHs). There is a wide range of SONELAHs in the U.S., from only 2 % of West Viriginians to 42% of Californians. Compared inside individual states, however, variations are less extreme. Read More
Heroin and Alcohol: Could there be a relationship?
Daphka Alius
Alcohol abuse is a disease that affects millions in the US. Similarly, opioids have become a national health crisis signaling a substantial increase in opioids use. The question under investigation is whether the same people who abuse heroin, a form of opioid, are also drinking congruously throughout the year. Using data from National Survey of Drug Use and Health, I found that people who infrequently (< 30 days/year) drink alcohol in a year are consuming heroin 1.7 times longer in a year than those who frequently (> 300 days/year) drink alcohol. Additionaly, the two variables are weakly correlated with a Pearson correlation that corresponds to -0.22. Read More
Does Health Insurance Type Lead To Opioid Addiction?
Micah Reid, Filipe Borba
The rate of opioid addiction has escalated into a crisis in recent years. Studies have linked health insurance with prescription painkiller overuse, but little has been done to investigate differences tied to health insurance type. We used data from the National Survey on Drug Use and Health from the year 2017 single out variations in drug use and abuse prevalence and duration across these groups. We found that while those with private health insurance were more likely to have used opioids than those with Medicaid/CHIP or no health insurance (57.3% compared to 45% and 47.4%, respectively), those with Medicaid/CHIP or no health insurance were more likely to have abused opioids when controlling for past opioid use (24.6% and 27.2% versus 17.6%, respectively). Those with private health insurance were also more likely to have used opioids in the past, while those with Medicaid/CHIP or no health insurance were more likely to have continued their use. This suggests that even though those with private health insurance are more likely to use opioids, those without are more likely to continue use and begin misuse once started on opiates. Read more
Finding differences between Conservatives and Liberals
Siddharth Garimella
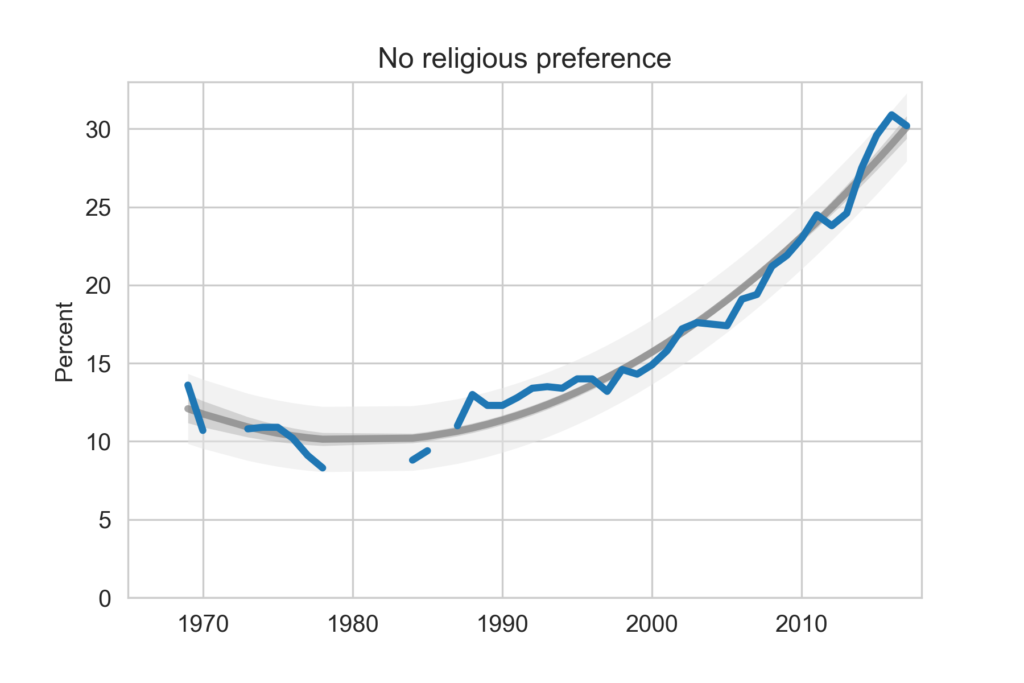
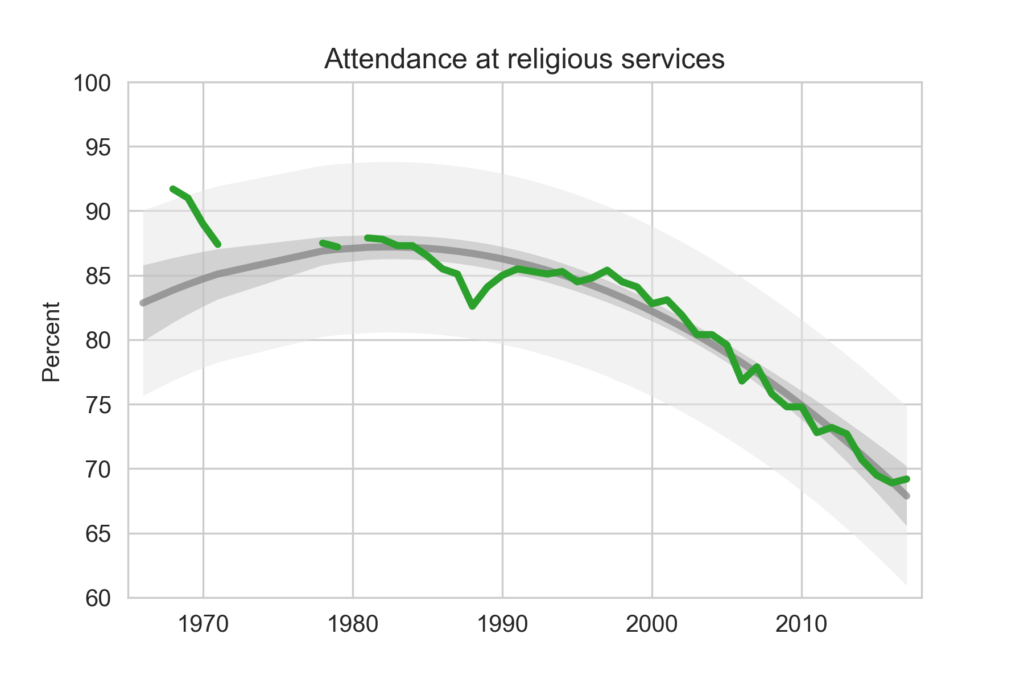
I looked through data from the General Social Survey (GSS) to gain a better understanding about what issues conservatives and liberals differ most on. After making some guesses of my own, I separated conservative and liberal respondents, and sorted their effect sizes for every variable in the dataset segment I had available, ultimately finding three big differences between the two groups. My results suggest conservatives most notably disagree more with same-sex relationships, tend to be slightly older, and attend religious events far more often than liberals do. Read more
Exploring OxyContin Use in the United States
Ariana Olson
According to the CDC, OxyContin is among the most common prescription opioids involved in overdose death. I explored variables related to OxyContin use, both medical and non-medical, from the 2014 National Survey on Drug Use and Health (NSDUH). I found that the median age that respondents tried OxyContin for the first time in a way that wasn’t prescribed for them is around 22, and that almost all respondents who had tried OxyContin non-medically did so before the age of 50. I also found that the overwhelming majority of respondents had never used OxyContin non-medically, but out of those who had, there was an 82% probability that they had used it over 12 months prior to the survey. People who used OxyContin also reported using the drug for fewer days total per year in a way that wasn’t prescribed to them than people who used it at all, prescribed or not. Finally, I found that the median age at which people first used OxyContin in a way that wasn’t directed by a doctor increased with older age groups, and the minimum age of first trying OxyContin non-medically per age group tended to increase as the age of the groups increased. Read more
Subjective Class Compared to Income Class
Cassandra Overney
Back in my hometown, many people consider themselves middle class regardless of their incomes. I grew up confusing income class with subjective class. Now that I am living in a new environment, I am curious to see whether a discrepancy between subjective and income class exists throughout America. The main question I want to answer is: how does subjective class compare to income class?
Income is not the only factor that Americans associate with class since most respondents consider themselves to be either working or middle class. However, there are some discernable differences in subjective class based on income. For example, respondents in the lowest income class are more likely to consider themselves working class than middle class (10.7% vs 6.3%) while respondents in the highest income class are more likely to consider themselves middle class than working class (13.3% vs 4.2%). Read more
The Contribution of the Opioid Epidemic on the Falling Life Expectancy in the United States
Sabrina Pereira
In recent years, a downward trend in the Average Life Expectancy (ALE) in the US has emerged. At the same time, the number of deaths by opioid poisoning has risen dramatically. Using mortality data from the Centers for Disease Control and Prevention, I create a model to quantify the effect of the increase of opioid-related deaths on the ALE in the US. According to the model, the ALE in 2017 would have been about .46 years higher if there had been no opioid-related deaths (79.06 years, compared to the observed 78.6 years). It is only recently that these deaths have created an observable effect this large. Read more
Exploring the Opioid Epidemic
Emma Price
People who use heroin are most likely to do so between the ages of 18 and 40, whereas people who misuse opiate pain relievers are consistently likely to misuse for the first time starting in their early teens. The portion of heroin and prescribed opiate users that stay in school until they complete high school is higher than that of people who do not use opiates; however, the portion of the population of heroin users drop very quickly in their likelihood to survive through college. The rate at which people who misuse opiate pain relievers drop out of school generally follows that of non-users once the high school tipping point is past. Read more
Drug use patterns and correlations
Sreekanth Reddy Sajjala
For users of various regulated substances, their exposure to and use of them varies greatly substance to substance. The National Survey on Drug Use and Health dataset has extensive data which can allow us to view patterns and correlations in their usage. Only 40% of the people who have ever tried cocaine have used it in the past year, but almost 60% of those who have tried heroin use it atleast once a week. People who have tried cannabis tend to try alcohol at an age 15% lower than users who haven’t tried cannabis do so. Unless drug use patterns change drastically, if someone has consumed cannabis at any point in their life they are over 20 times more likely to try heroin at some point in their life. Read more
Age and Generation Affect Happiness Levels in Marriage… A Little
Ashley Swanson
Among age, time, and cohort analysis, happiness levels in marriage are most drastically affected by the age of an individual up until their early 40’s. Between age 20 and age 40, the reported percentage of happy marriages drops by -0.45% percent a year, nearly 10% over the course of those two decades. The following 4 decades see a rebound of about 8%, meaning that 90-year-olds are nearly as happy as 20-year-olds, with those in their early 40’s experiencing the lowest levels of marital happiness. However, cohort effects have the highest explanatory value with an r-value of 0.44. Those born in 1950 experience 13.3% fewer happy marriages than those born in 1900, and those born in 2000 experience an average of 10.5% more happy marriages than those born in 1950. Each of these variables has a small effect size per year, a fraction of a percentage point, but the sustained trends over the decades are significant enough to have real effects. Read more
Associations between screen time and kids’ mental health
MinhKhang Vu
Previous research on children and adolescents has suggested strong associations between screen time and their mental health, contributing to growing concerns among parents, teachers, counselors and doctors about digital technology’s negative effects on children. Using the Census Bureau’s 2017 National Survey of Children’s Health (NSCH), I investigated a large (n=21,599) national random sample of 0- to 17-year-old children in the U.S. in 2017. The NSCH collects data on the physical and emotional health of American children every year, which includes information about their screen time usage and other comprehensive well-being measures. Children who spend 3 hours or more daily using computers are twice more likely to have an anxiety problem (CI 2.06 2.38) and four times more likely to experience depression (CI 3.97 5.11) than those who spend less than 3 hours. For kids spending 4 hours or more with computers, about 16% of them have some anxiety problems (CI 14.98 17.07), and 11% of them experience depression recently (CI 9.73 11.61). Along with the associations between screen time and diagnoses of anxiety and depression, how frequently a family has meals together also has strong linear relationships with both their children’s screen time and mental health. Children who do not have any meal with their family during the past week are twice more likely to have anxiety and three times more likely to experience depression than children who have meals with their family every day. However, in this study, I could not find any strong associations between the severity of kids’ mental illness and screen time, which leaves the open question, whether screen time directly affects children’s mental health. Read more