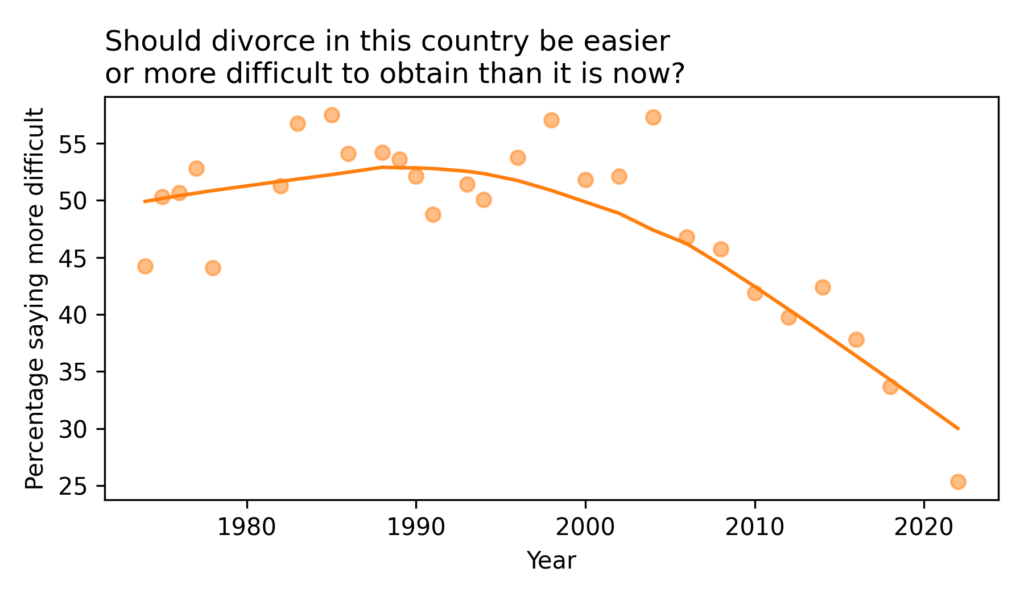
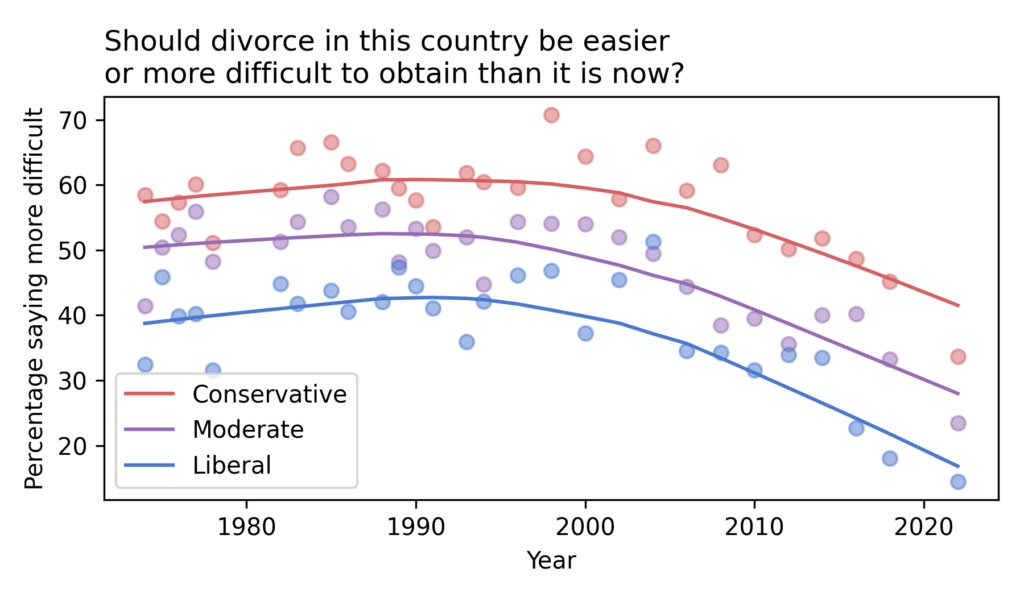
Have the Nones Leveled Off?

June 29, 2024 AllenDowney

Last month Ryan Burge published “The Nones Have Hit a Ceiling“, using data from the 2023 Cooperative Election Study to show that the increase in the number of Americans with no religious affiliation has hit a plateau. Comparing the number of Atheists, Agnostics, and “Nothing in Particular” between 2020 and 2023, he found that “the share of non-religious Americans has stopped rising in any meaningful way.”

When I read that, I was frustrated that the HERI Freshman Survey had not published new data since 2019. I’ve been following the rise of the “Nones” in that dataset since one of my first blog articles.

As you might guess, the Freshman Survey reports data from incoming college students. Of course, college students are not a representative sample of the U.S. population, and as rates of college attendance have increased, they represent a different slice of the population over time. Nevertheless, surveying young adults over a long interval provides an early view of trends in the general population.

Well, I have good news! I got a notification today that HERI has published data tables for the 2020 through 2023 surveys. They are in PDF, so I had to do some manual data entry, but I have results!

Religious preference

Among other questions, the Freshman Survey asks students to select their “current religious preference” from a list of seventeen common religions, “Other religion,” “Atheist”, “Agnostic”, or “None.”

The options “Atheist” and “Agnostic” were added in 2015. For consistency over time, I compare the “Nones” from previous years with the sum of “None”, “Atheist” and “Agnostic” since 2015.

The following figure shows the fraction of Nones from 1969, when the question was added, to 2023, the most recent data available.

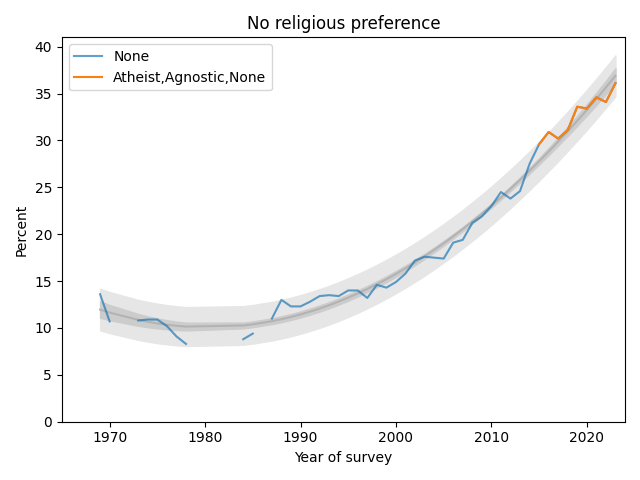
The blue line shows data until 2015; the orange line shows data from 2015 through 2019. The gray line shows a quadratic fit. The light gray region shows a 95% predictive interval.

The quadratic model continues to fit the data well and the recent trend is still increasing, but if you look at only the last few data points, there is some evidence that the rate of increase is slowing.

But not for women

Now here’s where things get interesting. Until recently, female students have been consistently more religious than male students. But that might be changing. The following figure shows the percentages of Nones for male and female students (with a missing point in 2018, when this breakdown was not available).

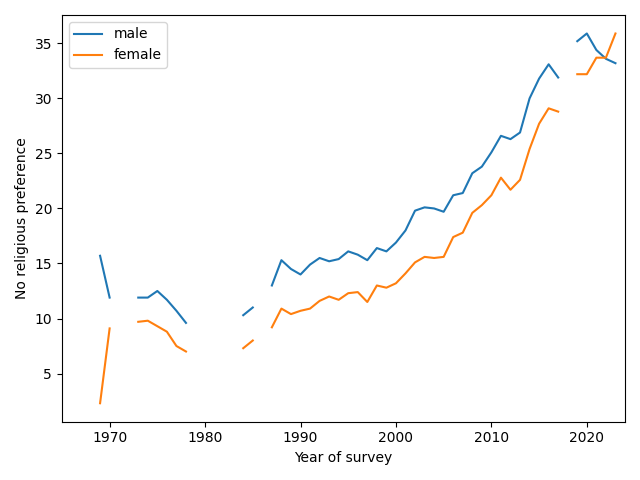
Since 2019, the percentage of Nones has increased for women and decreased for men, and it looks like women may now be less religious. So the apparent slowdown in the overall trend might be a mix of opposite trends in the two groups.

The following graph shows the gender gap over time, that is, the difference in percentages of male and female students with no religious affiliation.

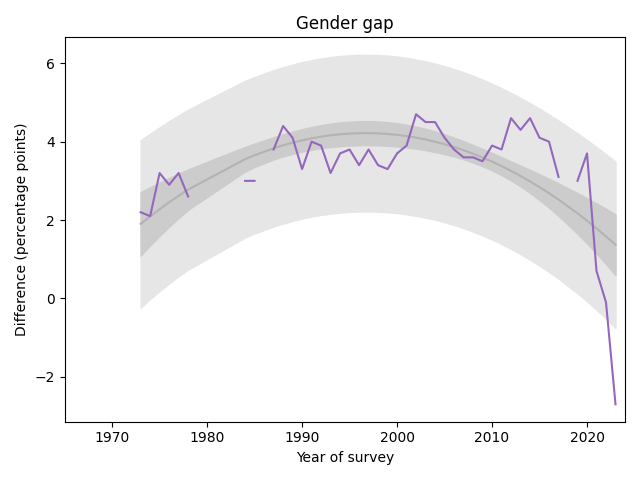
The gap was essentially unchanged from 1990 to 2020. But in the last three years it has changed drastically. It now falls outside the predictive range based on past data, which suggests a change this large would be unlikely by chance.

Similarly with attendance at religious services, the gender gap has closed and possibly reversed.

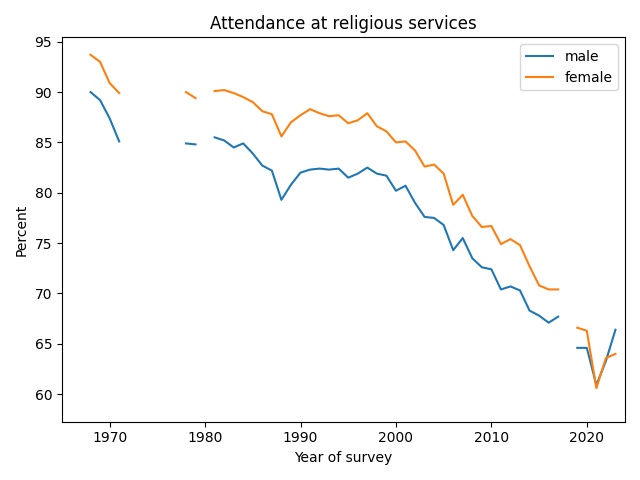
UPDATE: Ryan Burge looked at the gender gap in CES and GSS data and found similar results: especially among young people, the gender gap has either disappeared or crossed over. And Ryan pointed me to this article by Dan Cox and Kelsey Eyre Hammond which reports similar trends in data from the Survey Center on American Life.

Attendance

The survey also asks students how often they “attended a religious service” in the last year. The choices are “Frequently,” “Occasionally,” and “Not at all.” Respondents are instructed to select “Occasionally” if they attended one or more times, so a wedding or a funeral would do it.

The following figure shows the fraction of students who reported any religious attendance in the last year, starting in 1968. I discarded a data point from 1966 that seems unlikely to be correct.

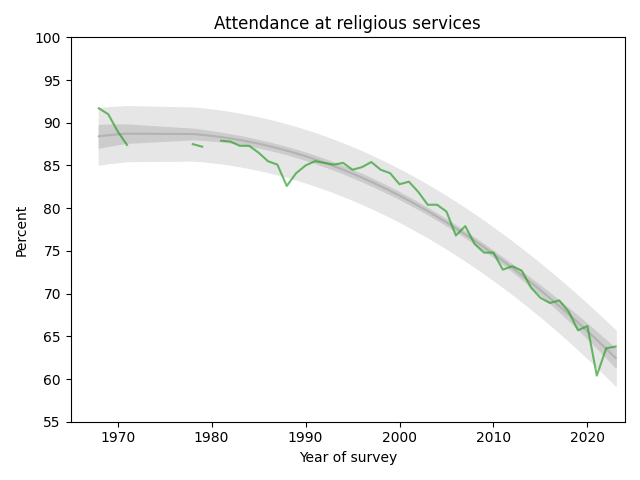
There is a clear dip in 2021, likely due to the pandemic, but the last two data points have returned to the long-term trend.

Data Source

The data reported here are available from the HERI publications page. Since I entered the data manually from PDF documents, it’s possible I have made errors.

Should divorce be more difficult?

June 14, 2024 AllenDowney

“The Christian right is coming for divorce next,” according to this recent Vox article, and “Some conservatives want to make it a lot harder to dissolve a marriage.”

As always when I read an article like this, I want to see data — and the General Social Survey has just the data I need. Since 1974, they have asked a representative sample of the U.S. population, “Should divorce in this country be easier or more difficult to obtain than it is now?” with the options to respond “Easier”, “More difficult”, or “Stay as is”.

Here’s how the responses have changed over time:

Since the 1990s, the percentage saying divorce should be more difficult has dropped from about 50% to about 30%. [The last data point, in 2022, may not be reliable. Due to disruptions during the COVID pandemic, the GSS changed some elements of their survey process — in the 2021 and 2022 data, responses to several questions have deviated from long-term trends in ways that might not reflect real changes in opinion.]

If we break down the results by political alignment, we can see whether these changes are driven by liberals, conservatives, or both.

Not surprisingly, conservatives are more likely than liberals to believe that divorce should be more difficult, by a margin of about 20 percentage points. But the percentages have declined in all groups — and fallen below 50% even among self-described conservatives.

As the Vox article documents, conservatives in several states have proposed legislation to make divorce more difficult. Based on the data, these proposals are likely to be unpopular.

To see my analysis, you can run this notebook on Colab. For similar analysis of other topics, see Chapter 11 of Probably Overthinking It.

Which Standard Deviation?

June 8, 2024 AllenDowney

It’s another installment in Data Q&A: Answering the real questions with Python. Previous installments are available from the Data Q&A landing page.

standard_dev

Which Standard Deviation?¶

Here’s a question from the Reddit statistics forum.

When do we use N and when N-1 for computation of sd and cov?

So I was doing a task, where I had a portfolio of shares and I was given their yields. Then I had to calculate [covariance], [standard deviation] etc. But I simply do not know when to use N and when N-1. I only know that it has to do something with degrees of freedom. Can someone explain it to me like to a 10 year old? Thanks!

If you look up the formula for standard deviation, you are likely to find two versions. One has the sample size, N, in the denominator; the other has N-1.

Sometimes the explanation of when you should use each of them is not clear. And to make it more confusing, some software packages compute the N version by default, and some the N-1 version.

Let’s see if we can straighten it all out.

Click here to run this notebook on Colab.

I’ll download a utilities module with some of my frequently-used functions, and then import the usual libraries.

In [1]:

from os.path import basename, exists

def download(url):
    filename = basename(url)
    if not exists(filename):
        from urllib.request import urlretrieve

        local, _ = urlretrieve(url, filename)
        print("Downloaded " + str(local))
    return filename

download('https://github.com/AllenDowney/DataQnA/raw/main/nb/utils.py')

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns

from utils import decorate

In [2]:

# install the empiricaldist library, if necessary

try:
    import empiricaldist
except ImportError:
    !pip install empiricaldist

Samples and Populations¶

Suppose we are given a sequence of numbers and asked to compute the standard deviation. As an example, we’ll use the sequence from 0 to 9.

In [3]:

N = 10
data = np.arange(N)
data

Out[3]:

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

The first step is to compute the mean.

In [4]:

m = np.mean(data)
m

Out[4]:

4.5

The deviations are the distances of each point from the mean.

In [5]:

deviations = data - m
deviations

Out[5]:

array([-4.5, -3.5, -2.5, -1.5, -0.5,  0.5,  1.5,  2.5,  3.5,  4.5])

Next we compute the sum of the squared deviations.

In [6]:

ssd = np.sum(deviations **2)
ssd

Out[6]:

82.5

Then we compute the variance — we’ll start with the version that has N in the denominator.

In [7]:

var = ssd / N

Finally, the standard deviation is the square root of variance.

In [8]:

std = np.sqrt(var)
std

Out[8]:

2.8722813232690143

And here’s the version with N-1 in the denominator.

In [9]:

var = ssd / (N-1)
std = np.sqrt(var)
std

Out[9]:

3.0276503540974917

With N=10, the difference between the version is non-negligible, but this is pretty much the worst case. With larger sample sizes, the difference in smaller — and with smaller sample sizes, you probably shouldn’t compute a standard deviation at all.

By default, NumPy computes the N version.

In [10]:

np.std(data)

Out[10]:

2.8722813232690143

But with the optional argument ddof=1, it computes the N-1 version.

In [11]:

np.std(data, ddof=1)

Out[11]:

3.0276503540974917

By default, Pandas computes the N-1 version.

In [12]:

pd.Series(data).std()

Out[12]:

3.0276503540974917

But with the optional argument ddof=0, it computes the N version.

In [13]:

pd.Series(data).std(ddof=0)

Out[13]:

2.8722813232690143

It is not ideal that the two libraries have different default behavior. And it might not be obvious why the parameter that controls this behavior is called ddof.

The answer is related to OP’s question about “degrees of freedom”. To understand that term, suppose I ask you to think of three numbers. You are free to choose any first number, any second number, and any third number. In that case, you have three degrees of freedom.

Now suppose I ask you to think of three numbers, but they are required to add up to 10. You are free to choose the first and second numbers, but then the third number is determined by the requirement. So you have only two degrees of freedom.

If we are given a dataset with N elements, we generally assume that it has N degrees of freedom unless we are told otherwise. That’s what the ddof parameter does. It stands for “delta degrees of freedom”, where “delta” indicates a change or a difference. In this case, it is the difference between the presumed degrees of freedom, N, and the degrees of freedom that should be used for the computation, N - ddof.

So, with ddof=0, the denominator is N. With ddof=1, the denominator is N-1.

Which one is right?¶

So when should you use one or the other? It depends on whether you are describing data or making a statistical inference.

The N version is a descriptive statistic — it is quantifies the variability of the data.
The N-1 version is an estimator — if data is a sample from a population, we can use it to infer the standard deviation of the population.

To be more specific, the N-1 version is an almost unbiased estimator, which means that it gets the answer almost right, on average, in the long run. Let’s see how that works.

Consider a uniform distribution from 0 to 10.

In [14]:

from scipy.stats import uniform

dist = uniform(0, 10)

Here are the actual mean and standard deviation of this distribution, computed analytically.

In [15]:

dist.mean(), dist.std()

Out[15]:

(5.0, 2.8867513459481287)

If we generate a large random sample from this distribution, we expect its standard deviation to be close to 2.9.

In [16]:

sample = dist.rvs(size=10000)
sample.std(ddof=0), sample.std(ddof=1)

Out[16]:

(2.8816683774305085, 2.881812471656537)

It is, and with a large sample size, the difference between the N version and the N-1 version is negligible.

But let’s see what happens if we generate small samples many times. First we’ll compute the N version of the standard deviation for 10001 samples.

In [17]:

standard_deviations_N = [dist.rvs(N).std(ddof=0) for i in range(10001)]

Ideally, the mean of these estimates should be close to the actual mean of the distribution, which is about 2.9.

In [18]:

np.mean(standard_deviations_N)

Out[18]:

2.6966272770954323

But it’s not — it is too low on average, which means it is a biased estimator.

Let’s see if the N-1 version is better.

In [19]:

standard_deviations_Nminus1 = [dist.rvs(N).std(ddof=1) for i in range(10001)]

np.mean(standard_deviations_Nminus1)

Out[19]:

2.8482429099753923

Yes! The N-1 version is a much less biased estimator of the standard deviation.

That’s why the N-1 version is called the “sample standard deviation”, because it is appropriate when we are using a sample to estimate the standard deviation of a population.

If, instead, we are able to measure an entire population, we can use the N version — which is why it is called the “population standard deviation”.

Should we care?¶

On one hand, it is impressive that such a simple correction yields a much better estimator. On the other hand, it almost never matters in practice.

If you have a large sample, the difference between the two versions is negligible.
If you have a small sample, you can’t make a precise estimate of the standard deviation anyway.

To demonstrate the second point, let’s look at the distributions of the estimates using the two versions.

In [20]:

sns.kdeplot(standard_deviations_N, label='N version')
sns.kdeplot(standard_deviations_Nminus1, label='N-1 version')

decorate(xlabel='Estimated standard deviation')

No description has been provided for this image

Compared to the variation in the estimates, the difference between the versions is small.

In summary, if your sample size is small and it is really important to avoid underestimating the standard deviation, use the N-1 correction. Otherwise it doesn’t matter.

In [23]:

data = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
np.std(data)

Out[23]:

2.8722813232690143

In [24]:

pd.Series(data).std()

Out[24]:

3.0276503540974917

Data Q&A: Answering the real questions with Python

License: Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International

What is a percentile rank?

June 1, 2024 AllenDowney

It’s another installment in Data Q&A: Answering the real questions with Python. Previous installments are available from the Data Q&A landing page.

percentile_rank

What is a Percentile Rank?¶

Here’s a question from the Reddit statistics forum.

What’s the difference between cumulative frequency as a percentage and percentiles?

Example that got me super confused:

[Here’s the data provided by OP]:

In [1]:

import pandas as pd

columns = ['score', 'frequency', 'cumulative frequency', 'cumulative percentage']

data = [
    (8, 1, 1, 2),
    (9, 1, 2, 4),
    (10, 1, 3, 6),
    (11, 3, 6, 13),
    (12, 5, 11, 23),
    (13, 7, 18, 38),
    (14, 8, 26, 54),
    (15, 9, 35, 73),
    (16, 6, 41, 85),
    (17, 4, 45, 94),
    (18, 2, 47, 98),
    (19, 1, 48, 100),
]
df = pd.DataFrame(data, columns=columns)
df

Out[1]:

	score	frequency	cumulative frequency	cumulative percentage
0	8	1	1	2
1	9	1	2	4
2	10	1	3	6
3	11	3	6	13
4	12	5	11	23
5	13	7	18	38
6	14	8	26	54
7	15	9	35	73
8	16	6	41	85
9	17	4	45	94
10	18	2	47	98
11	19	1	48	100

OP continues:

To me, the last [column], the “cumulative frequency” expressed in percentages is a percentile: it’s the percentage of scores lower then or the same as the score it’s calculated for.

However, in my class it’s explained that the percentile for score 14 would be 46, and that the percentile for score 17 would be 90, not 94.

The way they arrive at this is that upper and lower limits for the percentile calculation have to be set, in the case of score 14 that would be 14 and 13, and then the percentile would be calculated as (upper limit+lower limit)/2.

In the case of 14: (38+54)/2 = 46

This makes absolutely no sense to me: why are we introducing arbitrary limits to average out when the cumulative frequency in percentages, to me, seems to meet the definition of a percentile perfectly?

What’s at issue here is the definition of percentile and percentile rank. As an example, let’s consider the distribution of height, and suppose the median is 168 cm. In that case, 168 cm is the 50th percentile, and if someone is 168 cm tall, their percentile rank is 50%.

By this definition, the percentile rank for a particular quantity is its cumulative frequency expressed as a percentage, exactly as OP suggests. If you are taller than, or the same height as, 50% of the population, your percentile rank is 50%.

However, some classes teach the alternative definition OP presents. So, let me explain the two definitions, and we can discuss the pros and cons. At the risk of giving away the ending, here is my conclusion:

Percentiles and percentile ranks are perfectly well defined, and I don’t think we should encourage variations on the definitions.
In a dataset with many repeated values, percentile ranks might not measure what we want — in that case we might want to compute a different statistic, but then we should give it a different name.

In other words, I agree with OP.

Click here to run this notebook on Colab.

I’ll download a utilities module with some of my frequently-used functions, and then import the usual libraries.

In [2]:

from os.path import basename, exists

def download(url):
    filename = basename(url)
    if not exists(filename):
        from urllib.request import urlretrieve

        local, _ = urlretrieve(url, filename)
        print("Downloaded " + str(local))
    return filename

download('https://github.com/AllenDowney/DataQnA/raw/main/nb/utils.py')

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns

from utils import decorate

In [3]:

# install the empiricaldist library, if necessary

try:
    import empiricaldist
except ImportError:
    !pip install empiricaldist

Percentiles and percentile ranks¶

From the dataset OP provided, we can extract the scores and their frequencies.

In [4]:

pairs = df[['frequency', 'score']].values

And we can reconstitute the sample by making the given number of copies of each score.

In [5]:

sample = np.concatenate([[score] * freq for freq, score in pairs])
sample

Out[5]:

array([ 8,  9, 10, 11, 11, 11, 12, 12, 12, 12, 12, 13, 13, 13, 13, 13, 13,
       13, 14, 14, 14, 14, 14, 14, 14, 14, 15, 15, 15, 15, 15, 15, 15, 15,
       15, 16, 16, 16, 16, 16, 16, 17, 17, 17, 17, 18, 18, 19])

Now suppose we want to compute the median score and the interquartile range (IQR). We can use the NumPy function percentile to compute the 25th, 50th, and 75th percentiles.

In [6]:

np.percentile(sample, [25, 50, 75])

Out[6]:

array([13., 14., 16.])

So the median score is 14 and the IQR is 16 - 13 = 3.

Going in the other direction, if we are given a score, q, we can compute its percentile rank by computing the fraction of scores less than or equal to q, expressed as a percentage.

In [7]:

q = 14
np.mean(sample <= q) * 100

Out[7]:

54.166666666666664

If someone gets the median score of 14, their percentile rank is about 54%.

Here we see the first thing that bothers people about percentiles and percentile ranks: with a finite dataset, they are not invertible. If you compute the percentile rank of the 50th percentile, the answer is not always 50%. To see why, let’s consider the CDF.

The CDF¶

Percentiles and percentile ranks are closely related to the the cumulative distribution function (CDF). To demonstrate, we can use empiricaldist to make a Cdf object from the reconstituted sample.

In [8]:

from empiricaldist import Cdf

cdf = Cdf.from_seq(sample)
cdf

Out[8]:

	probs
8	0.020833
9	0.041667
10	0.062500
11	0.125000
12	0.229167
13	0.375000
14	0.541667
15	0.729167
16	0.854167
17	0.937500
18	0.979167
19	1.000000

A Cdf object is a Pandas Series that contains the observed quantities as an index and their cumulative probabilities as values. We can use square brackets to look up a quantity and get a cumulative probability.

In [9]:

cdf[14]

Out[9]:

0.5416666666666666

If we multiply by 100, we get the percentile rank.

But square brackets only work with quantities in the dataset. If we look up any other quantity, that’s an error. However, we can use parentheses to call the Cdf object like a function.

In [10]:

cdf(14)

Out[10]:

array(0.54166667)

And that works with any numerical quantity.

In [11]:

cdf(13.5)

Out[11]:

array(0.375)

Cdf provides a step method that plots the CDF as a step function, which is what it technically is.

In [12]:

cdf.step(label='')
decorate(ylabel='CDF')

To be more explicit, we can put markers at the top of each vertical segment to indicate how the function is evaluated at one of the observed quantities.

In [13]:

cdf.step(label='')
cdf.plot(style='o', label='')
decorate(ylabel='CDF')

The Cdf object provides a method called inverse that computes the inverse CDF — that is, if you give it a cumulative probability, it computes the corresponding quantity.

In [14]:

p1 = 0.375
cdf.inverse(p1)

Out[14]:

array(13.)

The result from an inverse lookup is sometimes called a “quantile”, which is the name of a Pandas method that computes quantiles.

If we put the sample into a Series, we can use quantile to compute the quantity to look up the cumulative probability p1.

In [15]:

sample_series = pd.Series(sample)
sample_series.quantile(p1)

Out[15]:

13.625

By default, quantile uses interpolates linearly between the observed values. If we want this function to behave according to the definition of the CDF, we have to specify a different kind of interpolation.

In [16]:

sample_series.quantile(p1, interpolation='lower')

Out[16]:

If the result from the inverse CDF is called a quantile, you might wonder what we call the result from the CDF. By analogy with percentile and percentile rank, I think it should be called a quantile rank, but no one calls it that. As far as I can tell, it’s just called a cumulative probability.

So what’s wrong with percentile rank?¶

Percentiles and percentile ranks have a perfectly good definition, which follows from the definition of the CDF. So what’s the problem? Well, I have to admit — the definition is a little arbitrary.

In the example, suppose your score is 14. Your score is strictly better than 37.5% of the other scores.

In [17]:

less = np.mean(sample < 14)
less

Out[17]:

0.375

It’s strictly worse than 45.8%

In [18]:

more = np.mean(sample > 14)
more

Out[18]:

0.4583333333333333

And equal to 16.7%.

In [19]:

same = np.mean(sample == 14)
same

Out[19]:

0.16666666666666666

So if we want a single number that quantifies your performance relative to the rest of the class, which number should we use?

The definition of the CDF suggests we should report the fraction of the class whose score is less than or equal to yours. But that is an arbitrary choice. We could just as easily report the fraction whose score is strictly less — or the midpoint of these extremes. For a score of 14, here’s the midpoint:

In [20]:

less + same / 2

Out[20]:

0.4583333333333333

That’s the result OP’s teacher was expecting, and to be fair, that’s Wikipedia’s definition of percentile rank. But I don’t like it.

Discussion¶

I prefer the CDF-based definition of percentile rank because it’s consistent with the way most computational tools work. The midpoint-based definition feels like a holdover from the days of working with small datasets by hand.

That’s just my preference — if people want to compute midpoints, I won’t stop them. But for the sake of clarity, we should give different names to different statistics.

Historically, I think the CDF-based definition has the stronger claim on the term “percentile rank”. For the midpoint-based definition, ChatGPT suggests “midpoint percentile rank” or “average percentile rank”. Those seem fine to me, but it doesn’t look like they are widely used.

Data Q&A: Answering the real questions with Python

License: Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International

Logarithms and Heteroskedasticity

May 26, 2024 AllenDowney

Here’s another installment in Data Q&A: Answering the real questions with Python. Previous installments are available from the Data Q&A landing page.

log_heterosked

Logarithms and heteroskedasticity¶

Here’s a question from the Reddit statistics forum.

Is it correct to use logarithmic transformation in order to mitigate heteroskedasticity?

For my studies I gathered data on certain preferences across a group of people. I am trying to figure out if I can pinpoint preferences to factors such as gender in this case.

I used mixed ANOVA analysis with good success however one of my hypothesis came up with heteroskedasticity when doing Levene’s test. [I’ve been] breaking my head all day on how to solve this. I’ve now used logarithmic transformation to all 3 test results and run another Levene’s. When using the media value the test now results [in] homoskedasticity, however interaction is no longer significant?

Is this the correct way to deal with this problem or is there something I am missing? Thanks in advance to everyone taking their time to help.

Although the question is about ANOVA, I’m going to reframe it in terms of regression, for two reasons:

Discussion of heteroskedasticity is clearer in the context of regression.
For many problems, a regression model is better than ANOVA anyway.

Click here to run this notebook on Colab.

I’ll download a utilities module with some of my frequently-used functions, and then import the usual libraries.

In [1]:

from os.path import basename, exists

def download(url):
    filename = basename(url)
    if not exists(filename):
        from urllib.request import urlretrieve

        local, _ = urlretrieve(url, filename)
        print("Downloaded " + str(local))
    return filename

download('https://github.com/AllenDowney/DataQnA/raw/main/nb/utils.py')

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns

from utils import decorate

In [2]:

# install the empiricaldist library, if necessary

try:
    import empiricaldist
except ImportError:
    !pip install empiricaldist

What is heteroskedasticity?¶

Linear regression is based on a model of the data-generating process where the independent variable y is the sum of

A linear function of x with an unknown slope and intercept, and
Random values drawn from a Gaussian distribution with mean 0 and unknown standard deviation, sigma, that does not depend on x.

If, contrary to the second assumption, sigma depends on x, the data-generating process is heteroskedastic. Some amount of heteroskedasticity is common in real data, but most of the time it’s not a problem, because:

Heteroskedasticity doesn’t bias the estimated parameters of the model, only the standard errors,
Even very strong heteroskedasticity doesn’t affect the standard errors by much, and
For practical purposes we don’t need standard errors to be particularly precise.

To demonstrate, let’s generate some data. First, we’ll draw xs from a normal distribution.

In [3]:

np.random.seed(17)

n = 200
xs = np.random.normal(30, 1, size=n)
xs.sort()

To generate heteroskedastic data, I’ll use interpolate to construct a function where sigma depends on x.

In [4]:

from scipy.interpolate import interp1d

def interpolate(xs, sigma_seq):
    return interp1d([xs.min(), xs.max()], sigma_seq)(xs)

To generate strong heteroskedasticity, I’ll vary sigma over a wide range.

In [5]:

sigmas = interpolate(xs, [0.1, 6.0])
np.mean(sigmas)

Out[5]:

3.126391153924031

Here’s what sigma looks like as a function of x.

In [6]:

plt.plot(xs, sigmas, '.')

decorate(xlabel='x',
         ylabel='sigma')

Now we can generate ys with variable values of sigma.

In [7]:

ys = xs + np.random.normal(0, sigmas)

If we make a scatter plot of the data, we see a cone shape that indicates heteroskedasticity.

In [8]:

plt.plot(xs, ys, '.')

decorate(xlabel='x', ylabel='y')

Now let’s fit a model to the data.

In [9]:

import statsmodels.api as sm

X = sm.add_constant(xs)
ols_model = sm.OLS(ys, X)
ols_results = ols_model.fit()

intercept, slope = ols_results.params
intercept, slope

Out[9]:

(0.7580177696902339, 0.9672433174107101)

Here’s what the fitted line looks like.

In [10]:

fys = intercept + slope * xs

plt.plot(xs, ys, '.')
plt.plot(xs, fys)

decorate(xlabel='x', ylabel='y')

If we plot the absolute values of the residuals, we can see the heteroskedasticity more clearly.

In [11]:

resid = ys - fys
plt.plot(xs, np.abs(resid), '.')

decorate(xlabel='x', ylabel='absolute residual')

Testing for heteroskedasticity¶

OP mentions using the Levene test for heteroskedasticity, which is used to test whether sigma is different between groups. For continuous values of x and y, we can use the Breusch-Pagan Lagrange Multiplier test:

In [12]:

from statsmodels.stats.diagnostic import het_breuschpagan

_, p_value, _, _ = het_breuschpagan(resid, ols_model.exog)
p_value

Out[12]:

0.0006411829020109725

Or White’s Lagrange Multiplier test:

In [13]:

from statsmodels.stats.diagnostic import het_white

_, p_value, _, _ = het_white(resid, ols_model.exog)
p_value

Out[13]:

0.0019263142806157931

Both tests produce small p-values, which means that if we generate a dataset by a homoskedastic process, there is almost no chance it would have as much heteroskedasticity as the dataset we generated.

If you have never heard of either of these tests, don’t panic — neither had I under I looked them up for this example. And don’t worry about remembering them, because you should never use them again. Like testing for normality, testing for heteroskedasticity is never useful.

Why? Because in almost any real dataset, you will find some heteroskedasticity. So if you test for it, there are only two possible results:

If the heteroskedasticity is small and you don’t have much data, you will fail to reject the null hypothesis.
If the heteroskedasticity is large or you have a lot of data, you will reject the null hypothesis.

Either way, you learn nothing — and in particular, you don’t learn the answer to the question you actually care about, which is whether the heteroskedasticity is so large that the effect on the standard errors is large enough that you should care.

And the answer to that question is almost always no.

Should we care?¶

The dataset we generated has very large heteroskedasticity. Let’s see how much effect that has on the results. Here are the standard errors from simple linear regression:

In [14]:

ols_results.bse

Out[14]:

array([6.06159018, 0.20152957])

Now, there are several ways to generate standard errors that are robust in the presence of heteroskedasticity. One is the Huber-White estimator, which we can compute like this:

In [15]:

robust_se = ols_results.get_robustcov_results(cov_type='HC3')
robust_se.bse

Out[15]:

array([6.73913518, 0.2268012 ])

Another is to use Huber regression.

In [16]:

huber_model = sm.RLM(ys, X, M=sm.robust.norms.HuberT())
huber_results = huber_model.fit()
huber_results.bse

Out[16]:

array([5.92709031, 0.19705786])

Another is to use quantile regression.

In [17]:

quantile_model = sm.QuantReg(ys, X)
quantile_results = quantile_model.fit(q=0.5)
quantile_results.bse

Out[17]:

array([7.6449323 , 0.25417092])

And one more option is a wild bootstrap, which resamples the residuals by multiplying them by a random sequence of 1 and -1. This way of resampling preserves heteroskedasticity, because it only changes the sign of the residuals, not the magnitude, and it maintains the relationship between those magnitudes and x.

In [18]:

from scipy.stats import linregress

def wild_bootstrap():
    resampled = fys + ols_results.resid * np.random.choice([1, -1], size=n)
    res = linregress(xs, resampled)
    return res.intercept, res.slope

We can use wild_bootstrap to generate a sample from the sampling distributions of the intercept and slope.

In [19]:

sample = [wild_bootstrap() for i in range(1001)]

The standard deviation of the sampling distributions is the standard error.

In [20]:

bootstrap_bse = np.std(sample, axis=0)
bootstrap_bse

Out[20]:

array([6.63622313, 0.22341784])

Now let’s put all of the result in a table.

In [21]:

columns = ['SE(intercept)', 'SE(slope)']
index = ['OLS', 'Huber-White', 'Huber', 'quantile', 'bootstrap']
data = [ols_results.bse, robust_se.bse, huber_results.bse, 
        quantile_results.bse, bootstrap_bse]
df = pd.DataFrame(data, columns=columns, index=index)
df.sort_values(by='SE(slope)')

Out[21]:

	SE(intercept)	SE(slope)
Huber	5.927090	0.197058
OLS	6.061590	0.201530
bootstrap	6.636223	0.223418
Huber-White	6.739135	0.226801
quantile	7.644932	0.254171

The standard errors we get from different methods are notably different, but the differences probably don’t matter.

First, I am skeptical of the results from Huber regression. With this kind of heteroskedasticity, the standard errors should be larger than what we get from OLS. I’m not sure what’s the problem is, and I haven’t bothered to find out, because I don’t think Huber regression is necessary in the first place.

The results from bootstrapping and the Huber-White estimator are the most reliable — which suggests that the standard errors from quantile regression are too big.

In my opinion, we don’t need esoteric methods to deal with heteroskedasticity. If heteroskedasticity is extreme, consider using wild bootstrap. Otherwise, just use ordinary least squares.

Now let’s address OP’s headline question, “Is it correct to use logarithmic transformation in order to mitigate heteroskedasticity?”

Log transform help?¶

In some cases, a log transform can reduce or eliminate heteroskedasticity. However, there are several reasons this is not a good idea in general:

As we’ve seen, heteroskedasticity is not a big problem, so it usually doesn’t require any mitigation.
Taking a log transform of one or more variables in a regression model changes the meaning of the model — it hypothesizes a relationship between the variables that might not make sense in context.
Anyway, taking a log transform doesn’t always help.

To demonstrate the last point, let’s see what happens if we apply a log transform to the dependent variable:

In [22]:

log_ys = np.log10(ys)

Here’s what the scatter plot looks like after the transform.

In [23]:

plt.plot(xs, log_ys, '.')

decorate(xlabel='x', ylabel='log10 y')

Here’s what we get if we fit a model to the data.

In [24]:

ols_model_log = sm.OLS(log_ys, X)
ols_results_log = ols_model_log.fit()

intercept, slope = ols_results_log.params
intercept, slope

Out[24]:

(1.072059757295944, 0.013315487289434717)

And here’s the fitted line.

In [25]:

log_fys = intercept + slope * xs

plt.plot(xs, log_ys, '.')
plt.plot(xs, log_fys)

decorate(xlabel='x', ylabel='log10 y')

If we plot the absolute values of the residuals, we can see that the log transform did not entirely remove the heteroskedasticity.

In [26]:

log_resid = log_ys - log_fys
plt.plot(xs, np.abs(log_resid), '.')

decorate(xlabel='x', ylabel='absolute residual on log y')

Which we can confirm by running the tests again (which we should never do).

In [27]:

_, p_value, _, _ = het_breuschpagan(log_resid, ols_model_log.exog)
p_value

Out[27]:

0.002154782205265498

In [28]:

_, p_value, _, _ = het_white(log_resid, ols_model_log.exog)
p_value

Out[28]:

0.006069762292696221

The p-values are bigger, which suggests that the log transform mitigated the heteroskedasticity a little. But if the goal was to eliminate heteroskedasticity, the log transform didn’t do it.

Discussion¶

To summarize:

Heteroskedasticity is common in real datasets — if you test for it, you will often find it, provided you have enough data.
Either way, testing does not answer the question you really care about, which is whether the heteroskedasticity is extreme enough to be a problem.
Plain old linear regression is robust to heteroskedasticity, so unless it is really extreme, it is probably not a problem.
Even in the worst case, heteroskedasticity does not bias the estimated parameters — it only affects the standard errors — and we don’t need standard errors to be particularly precise anyway.
Although a log transform can sometimes mitigate heteroskedasticity, it doesn’t always succeed, and even if it does, it’s usually not necessary.
A log transform changes the meaning of the regression model in ways that might not make sense in context.

So, use a log transform if it makes sense in context, not to mitigate a problem that’s not much of a problem in the first place.

Data Q&A: Answering the real questions with Python

License: Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International

In [ ]:

Combining Risks

May 24, 2024 AllenDowney

Here’s another installment in Data Q&A: Answering the real questions with Python. Previous installments are available from the Data Q&A landing page.

combine_risk

Combining Risks¶

Here’s a question from the Reddit statistics forum.

Bit of a weird one but I’m hoping you’re the community to help. I work in children’s residential care and I’m trying to find a way of better matching potential young people together.

The way we calculate individual risk for a child is

risk = likelihood + impact (R=L+I), so

L4 + I5 = R9

That works well for individuals but I need to work out a good way of calculating a combined risk to place children [in] the home together. I’m currently using the [arithmetic] average but I don’t feel that it works properly as the average is always lower then the highest risk.

I’ll use a fairly light risk as an example, running away from the home. (We call this MFC missing from care) It’s fairly common that one of the kids will run away from the home at some point or another either out of boredom or frustration. If young person A has a risk of 9 and young person B has a risk of 12 the the average risk of MFC in the home would be 10.5

HOWEVER more often then not having two young people that go MFC will often result in more episodes as they will run off together, so having a lower risk rating doesn’t really make sense. Adding the two together to 21 doesn’t really work either though as the likelihood is the thing that increases not necessarily the impact.

I’m a lot better at chasing after run away kids then I am mathematics so please help 😂.

Here’s one way to think about this question: based on background knowledge and experience, OP has qualitative ideas about what happens when we put children at different risks together, and he is looking for a statistical summary that is consistent with these ideas.

The arithmetic mean probably makes sense as a starting point, but it clashes with the observation that if you put two children together who are high risk, they interact in ways that increase the risk. For example, if we put together children with risks 9 and 12, the average is 10.5, and OP’s domain knowledge says that’s too low — it should be more than 12.

At the other extreme, I’ll guess that putting together two low risk children might be beneficial to both — so the combined risk might be lower than either.

And that implies that there is a neutral point somewhere in the middle, where the combined risk is equal to the individual risks.

To construct a summary statistic like that, I suggest a weighted sum of the arithmetic and geometric means. That might sound strange, but I’ll show that it has the properties we want. And it might not be as strange as it sounds — there’s a reason it might make sense.

Click here to run this notebook on Colab.

I’ll download a utilities module with some of my frequently-used functions, and then import the usual libraries.

In [18]:

from os.path import basename, exists

def download(url):
    filename = basename(url)
    if not exists(filename):
        from urllib.request import urlretrieve

        local, _ = urlretrieve(url, filename)
        print("Downloaded " + str(local))
    return filename

download('https://github.com/AllenDowney/DataQnA/raw/main/nb/utils.py')

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns

from utils import decorate

In [19]:

# install the empiricaldist library, if necessary

try:
    import empiricaldist
except ImportError:
    !pip install empiricaldist

Weighted sum of means¶

The following function computes the arithmetic mean of a sequence of values, which is the sum divided by n.

In [20]:

def amean(xs):
    n = len(xs)
    return np.sum(xs) / n

The following function computes the geometric mean of a sequence, which is the product raised to the power 1/n.

In [21]:

def gmean(xs):
    n = len(xs)
    return np.prod(xs) ** (1/n)

And the following function computes the weighted sum of the arithmetic and geometric means. The constant k determines how much weight we give the geometric mean.

In [22]:

def mean_plus_gmean(*xs, k=1):
    return amean(xs) + k * (gmean(xs) - 4)

The value 4 determines the neutral point. So if we put together two people with risk 4, the combined average is 4.

In [23]:

mean_plus_gmean(4, 4)

Out[23]:

4.0

Above the neutral point, there is a penalty if we put together two children with higher risks.

In [24]:

mean_plus_gmean(5, 5)

Out[24]:

6.0

In that case, the combined risk is higher than the individual risks. Below the neutral point, there is a bonus if we put together two children with low risks.

In [25]:

mean_plus_gmean(3, 3)

Out[25]:

2.0

In that case, the combined risk is less than the individual risks.

If we combine low and high risks, the discrepancy brings the average down a little.

In [26]:

mean_plus_gmean(3, 5)

Out[26]:

3.872983346207417

In the example OP presented, where we put together two people with high risk, the penalty is substantial.

In [27]:

mean_plus_gmean(9, 12)

Out[27]:

16.892304845413264

If that penalty seems too high, we can adjust the weight, k, and the neutral point accordingly.

This behavior extends to more than two people. If everyone is neutral, the result is neutral.

In [28]:

mean_plus_gmean(4, 4, 4)

Out[28]:

3.9999999999999996

If you add one person with higher risk, there’s a moderate penalty, compared to the arithmetic mean.

In [29]:

mean_plus_gmean(4, 4, 5), amean([4, 4, 5])

Out[29]:

(4.6422027133971, 4.333333333333333)

With two higher risk people, the penalty is bigger.

In [30]:

mean_plus_gmean(4, 5, 5), amean([4, 5, 5])

Out[30]:

(5.308255500279445, 4.666666666666667)

And with three it is even bigger.

In [31]:

mean_plus_gmean(5, 5, 5), amean([5, 5, 5])

Out[31]:

(5.999999999999999, 5.0)

Does this make any sense?¶

The idea behind this suggestion is logistic regression with an interaction term. Let me explain where that comes from. OP explained:

The way we calculate individual risk for a child is

risk = likelihood + impact (R=L+I), so

L4 + I5 = R9

At first I thought it was strange to add a likelihood and an impact score, Thinking about expected value, I thought it should be the product of a probability and a cost. But if both are on a log scale, adding these logarithms is like multiplying probability by impact on a linear scale, so that makes more sense.

And if the scores are consistent with something like a log-odds scale, we can see a connection with logistic regression. If r1 and r2 are risk scores, we can imagine a regression equation that looks like this, where p is the probability of an outcome like “missing from care”:

logit(p) = a r1 + b r2 + c r1 r2

In this equation, logit(p) is the combined risk score, a, b, and c are unknown parameters, and the product r1 r2 is an interaction term that captures the tendency of high risks to amplify each other.

With enough data, we could estimate the unknown parameters. Without data, the best we can do is chose values that make the results consistent with expectations.

Since r1 and r2 are interchangeable, they have to have the same parameter. And since the whole risk scale has an unspecified zero point, we can set it a and b to 1/2. Which means there is only one parameter left, the weight of the interaction term.

logit(p) = (r_1 + r2) / 2 + k r1 r2

Now we can see that the first term is the arithmetic mean and the second term is close to the geometric mean, but without the square root.

So the function I suggested — the weighted sum of arithmetic and weighted means — is not identical to the logistic model, but it is motivated by it.

With this rationale in mind, we might consider a revision: rather than add the likelihood and impact scores, and then compute the weighted sum of means, it might make more sense to separate likelihood and impact, compute the weighted sum of the means of the likelihoods, and then add back the impact.

Computing by hand¶

In case the Python code makes it hard to see what’s going on, let’s work an example by hand. Suppose r1 is 9 and r2 is 12.

In [32]:

r1 = 9
r2 = 12

Here’s the arithmetic mean.

In [33]:

m1 = (9 + 12) / 2
m1

Out[33]:

10.5

Here’s the geometric mean.

In [34]:

m2 = np.sqrt(9 * 12)
m2

Out[34]:

10.392304845413264

And here’s how we combine them.

In [35]:

k = 1
combined_risk = m1 + k * (m2 - 4)
combined_risk

Out[35]:

16.892304845413264

Discussion¶

This question got my attention because OP is working on a challenging and important problem — and they provided useful context. It’s an intriguing idea to define something that is intuitively like an average, but is not always bounded between the minimum and maximum of the data.

If we think strictly about generalized means, that’s not possible. But if we think in terms of logarithms, regression, and interaction terms, we find a way.

Data Q&A: Answering the real questions with Python

License: Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International

Bertrand’s Boxes

May 20, 2024 AllenDowney

An early draft of Probably Overthinking It included two chapters about probability. I still think they are interesting, but the other chapters are really about data, and the examples in these chapters are more like brain teasers — so I’ve saved them for another book. Here’s an excerpt from the chapter on Bayes theorem.

In 1889 Joseph Bertrand posed and solved one of the oldest paradoxes in probability. But his solution is not quite correct – it is right for the wrong reason.

The original statement of the problem is in his Calcul des probabilités (Gauthier-Villars, 1889). As a testament to the availability of information in the 21st century, I found a scanned copy of the book online and pasted a screenshot into an online OCR server. Then I pasted the French text into an online translation service. Here is the result, which I edited lightly for clarity:

Three boxes are identical in appearance. Each has two drawers, each drawer contains a medal. The medals in the first box are gold; those in the second box, silver; the third box contains a gold medal and a silver medal.

We choose a box; what is the probability of finding, in its drawers, a gold coin and a silver coin?

Three cases are possible and they are equally likely because the three chests are identical in appearance. Only one case is favorable. The probability is 1/3.

Having chosen a box, we open a drawer. Whatever medal one finds there, only two cases are possible. The drawer that remains closed may contain a medal whose metal may or may not differ from that of the first. Of these two cases, only one is in favor of the box whose parts are different. The probability of having got hold of this set is therefore 1/2.

How can it be, however, that it will be enough to open a drawer to change the probability and raise it from 1/3 to 1/2? The reasoning cannot be correct. Indeed, it is not.

After opening the first drawer, two cases remain possible. Of these two cases, only one is favorable, this is true, but the two cases do not have the same likelihood.

If the coin we saw is gold, the other may be silver, but we would be better off betting that it is gold.

Suppose, to show the obvious, that instead of three boxes we have three hundred. One hundred contain two gold medals, one hundred and two silver medals and one hundred one gold and one silver. In each box we open a drawer, we see therefore three hundred medals. A hundred of them are in gold and a hundred in silver, that is certain; the hundred others are doubtful, they belong to boxes whose parts are not alike: chance will regulate the number.

We must expect, when opening the three hundred drawers, to see less than two hundred gold coins the probability that the first that appears belongs to one of the hundred boxes of which the other coin is in gold is therefore greater than 1/2.

Now let me translate the paradox one more time to make the apparent contradiction clearer, and then we will resolve it.

Suppose we choose a random box, open a random drawer, and find a gold medal. What is the probability that the other drawer contains a silver medal? Bertrand offers two answers, and an argument for each:

Only one of the three boxes is mixed, so the probability that we chose it is 1/3.
When we see the gold coin, we can rule out the two-silver box. There are only two boxes left, and one of them is mixed, so the probability we chose it is 1/2.

As with so many questions in probability, we can use Bayes theorem to resolve the confusion. Initially the boxes are equally likely, so the prior probability for the mixed box is 1/3.

When we open the drawer and see a gold medal, we get some information about which box we chose. So let’s think about the likelihood of this outcome in each case:

If we chose the box with two gold medals, the likelihood of finding a gold medal is 100%.
If we chose the box with two silver medals, the likelihood is 0%.
And if we chose the box with one of each, the likelihood is 50%.

Putting these numbers into a Bayes table, here is the result:

	Prior	Likelihood	Product	Posterior
Two gold	1/3	1	1/3	2/3
Two silver	1/3	0	0	0
Mixed	1/3	1/2	1/6	1/3

The posterior probability of the mixed box is 1/3. So the first argument is correct. Initially, the probability of choosing the mixed box is 1/3 – opening a drawer and seeing a gold coin does not change it. And the Bayesian update tells us why: if there are two gold coins, rather than one, we are twice as likely to see a gold coin.

The second argument is wrong because it fails to take into account this difference in likelihood. It’s true that there are only two boxes left, but it is not true that they are equally likely. This error is analogous to the base rate fallacy, which is the error we make if we only consider the likelihoods and ignore the prior probabilities. Here, the second argument is wrong because it commits the a “likelihood fallacy” – considering only the prior probabilities and ignoring the likelihoods.

Right for the wrong reason

Bertrand’s resolution of the paradox is correct in the sense that he gets the right answer in this case. But his argument is not valid in general. He asks, “How can it be, however, that it will be enough to open a drawer to change the probability…”, implying that it is impossible in principle.

But opening the drawer does change the probabilities of the other two boxes. Having seen a gold coin, we rule out the two-silver box and increase the probability of the two-gold box. So I don’t think we can dismiss the possibility that opening the drawer could change the probability of the mixed box. It just happens, in this case, that it does not.

Let’s consider a variation of the problem where there are three drawers in each box: the first box contains three gold medals, the second contains three silver, and the third contains two gold and one silver.

In that case the likelihood of seeing a gold coin is each case is 1, 0, and 2/3, respectively. And here’s what the update looks like:

	Prior	Likelihood	Product	Posterior
Three gold	1/3	1	1/3	3/5
Three silver	1/3	0	0	0
Two gold, one silver	1/3	2/3	2/9	2/5

Now the posterior probability of the mixed box is 2/5, which is higher than the prior probability, which was 1/3. In this example, opening the drawer provides evidence that changes the probabilities of all three boxes.

I think there are two lessons we can learn from this example. The first is, don’t be too quick to assume that all cases are equally likely. The second is that new information can change probabilities in ways that are not obvious. The key is to think about the likelihoods.

Estimation with Small Samples

May 14, 2024 AllenDowney

Here’s another installment in Data Q&A: Answering the real questions with Python. Previous installments are available from the Data Q&A landing page.

gauss_bayes

Estimation with Small Samples¶

Here’s a question from the Reddit statistics forum.

Hey, so imagine I only have 6 samples from a value that has a normal distribution. Can I estimate the range of likely distributions from those 6?

Let’s be more specific. I’m considering the accuracy of a blood testing device. I took 6 samples of my blood at the same time from the same vein and gave them to the machine. The results are not all the same (as expected), indicating the device’s inherent level of imprecision.

So, I’m wondering if there’s a way to estimate the range of possibilities of what I would see if I could give 100 or 1000 samples?

I’m comfortable assuming a normal distribution around the “true” value. Is there any stats method to guesstimate the range of likely values for sigma? Or would I just need to drain my blood dry to get 1000 samples to figure that out?

Fyi, not a statistician.

Because the sample size is so small, this question cries out for a Bayesian approach. Why?

Bayesian methods do a good job of taking advantage of background information and extracting as much information as possible from the data,
With a small sample size, the uncertainty of the result is large, so it is important to quantify it, and
The motivating question is explicitly about making probabilistic predictions, which is what Bayesian methods do and classical methods don’t.

As an example, OP suggested looking at blood potassium (K+) levels, with the following data:

4.0, 3.9, 4.0, 4.0, 4.7, 4.2 (mmol/L)

OP also explained that the blood samples were collected “continuously from a single puncture … within seconds, not minutes,” so we don’t expect the true level to change much between samples. In that case, the variation in the measurements would largely reflect the precision of the testing device.

With that assumption, let’s see what we can do.

Click here to run this notebook on Colab.

I’ll download a utilities module with some of my frequently-used functions, and then import the usual libraries.

In [1]:

from os.path import basename, exists

def download(url):
    filename = basename(url)
    if not exists(filename):
        from urllib.request import urlretrieve

        local, _ = urlretrieve(url, filename)
        print("Downloaded " + str(local))
    return filename

download('https://github.com/AllenDowney/DataQnA/raw/main/nb/utils.py')

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns

from utils import decorate

In [2]:

# install the empiricaldist library, if necessary

try:
    import empiricaldist
except ImportError:
    !pip install empiricaldist

Bayesian estimation¶

Here’s the data.

In [3]:

data = [4.0, 3.9, 4.0, 4.0, 4.7, 4.2]
np.mean(data), np.std(data)

Out[3]:

(4.133333333333334, 0.2687419249432851)

Now we need prior distributions for mu and sigma. For the prior distribution of mu we can use the distribution in the general population. The “normal range” for potassium — which is usually the 5th and 95th percentiles of the population — is 3.5 to 5.4 mmol/L. So we can construct a normal distribution with these percentiles.

In [4]:

from scipy.stats import norm

hyper_mu = (3.5 + 5.4) / 2
hyper_sigma = 0.6

dist = norm(hyper_mu, hyper_sigma)
dist.ppf([0.05, 0.95])

Out[4]:

array([3.46308782, 5.43691218])

Now I’ll make a Pmf object that represents this distribution.

In [5]:

mus = np.linspace(2, 7, 51)
ps = dist.pdf(mus)

In [6]:

from empiricaldist import Pmf

prior_mu = Pmf(ps, mus)
prior_mu.index.name = 'mu'
prior_mu.normalize()

Out[6]:

9.99977690541445

In [7]:

prior_mu.plot(label='prior')
decorate(ylabel='PDF')

For the prior distribution of sigma, we could use some background information about the device. For example, based on similar devices, what values of sigma would be expected? I’ll use a gamma distribution to construct a prior PMF, but it could be anything.

In [8]:

from scipy.stats import gamma

alpha = 2
beta = 0.5

sigmas = np.linspace(0.01, 5, 101)
ps = gamma(alpha, scale=beta).pdf(sigmas)

In [9]:

prior_sigma = Pmf(ps, sigmas)
prior_sigma.index.name = 'sigma'
prior_sigma.normalize()

Out[9]:

20.03019853279729

In [10]:

prior_sigma.plot(label='prior')
decorate(ylabel='PDF')

This distribution represents the background knowledge that we expect the standard deviation to be less than 2, and we’d be surprised by anything much higher than that.

I’ll use this function to make a Pandas DataFrame to represent the joint prior.

In [11]:

def make_joint(s1, s2):
    """Compute the outer product of two Series.

    First Series goes across the columns;
    second goes down the rows.

    s1: Series
    s2: Series

    return: DataFrame
    """
    X, Y = np.meshgrid(s1, s2, indexing='ij')
    return pd.DataFrame(X*Y, index=s1.index, columns=s2.index)

In [12]:

prior = make_joint(prior_mu, prior_sigma)
prior.shape

Out[12]:

(51, 101)

I’ll use the following function to make a contour plot of the prior.

In [13]:

def plot_contour(joint):
    """Plot a joint distribution.

    joint: DataFrame representing a joint PMF
    """
    low = joint.to_numpy().min()
    high = joint.to_numpy().max()
    levels = np.linspace(low, high, 6)
    levels = levels[1:]

    cs = plt.contour(joint.columns, joint.index, joint, levels=levels, linewidths=1)
    decorate(xlabel=joint.columns.name,
             ylabel=joint.index.name)
    return cs

In [14]:

plot_contour(prior)
decorate()

The update¶

To use the data to update the prior, we have to compute the likelihood of the data for each possible pair of mu and sigma. Can can do that by creating a 3-D mesh with the possible values of mu and sigma, and the observed values of the data.

In [15]:

MU, SIGMA, DATA = np.meshgrid(prior_mu.index, prior_sigma.index, data,
                              indexing='ij')
MU.shape

Out[15]:

(51, 101, 6)

Now we can evaluate the normal distribution for each data point and each pair of mu and sigma.

In [16]:

densities = norm(MU, SIGMA).pdf(DATA)
densities.shape

Out[16]:

(51, 101, 6)

The likelihood of each pair is the product of the densities for the data points.

In [17]:

likelihood = densities.prod(axis=2)
likelihood.shape

Out[17]:

(51, 101)

The unnormalized posterior is the product of the prior and the likelihood.

In [18]:

posterior = prior * likelihood

We can normalize it like this.

In [19]:

def normalize(joint):
    """Normalize a joint distribution.

    joint: DataFrame
    """
    prob_data = joint.to_numpy().sum()
    joint /= prob_data
    return prob_data

In [20]:

normalize(posterior)
posterior.shape

Out[20]:

(51, 101)

And here’s what the result looks like.

In [21]:

plot_contour(posterior)
decorate()

Here’s the posterior distribution of sigma compared to the prior.

In [22]:

def marginal(joint, axis):
    """Compute a marginal distribution.

    axis=0 returns the marginal distribution of the first variable
    axis=1 returns the marginal distribution of the second variable

    joint: DataFrame representing a joint distribution
    axis: int axis to sum along

    returns: Pmf
    """
    return Pmf(joint.sum(axis=axis))

In [23]:

posterior_sigma = marginal(posterior, 0)

In [24]:

prior_sigma.plot(color='gray', label='prior')
posterior_sigma.plot(label='posterior')

decorate(xlabel='sigma', ylabel='PDF')

The posterior mean of sigma is about 0.4, somewhat higher than the standard deviation of the data.

In [25]:

posterior_sigma.mean(), np.std(data)

Out[25]:

(0.40440859064493323, 0.2687419249432851)

Predictions¶

The last part of OP’s question is “So, I’m wondering if there’s a way to estimate the range of possibilities of what I would see if I could give 100 or 1000 samples?”

We can simulate a future experiment with larger sample size by drawing random pairs from the joint posterior distribution and generating simulated measurements. That’s easier to do if we stack the posterior PMF.

In [26]:

posterior_pmf = Pmf(posterior.stack())
posterior_pmf.head()

Out[26]:

		probs
mu	sigma
2.0	0.0100	0.0
	0.0599	0.0
	0.1098	0.0

Now we can use NumPy’s choice function to choose a random pair of mu and sigma. For each random pair, we can generate 1000 simulated measurements from a normal distribution, and plot the distribution of the results.

In [27]:

for i in range(11):
    mu, sigma = np.random.choice(posterior_pmf.index, p=posterior_pmf)
    sample = np.random.normal(mu, sigma, size=1000)
    sns.kdeplot(sample, alpha=0.3)
    
decorate(xlabel='K+ (mmol/L)')

Each line shows the distribution of a possible sample of 1000 measurements. You can see that they vary in both location and spread, due to the uncertainty represented by the posterior distribution of mu and sigma.

Discussion¶

The normal distribution is probably a good enough model for this data, but for some pairs of mu and sigma in the prior, the normal distribution extends into negative values with non-negligible probability — and for measurements like these, negative values are nonsensical.

An alternative would be to run the whole calculation with the logarithms of the measurements. In effect, this would model the distribution of the data as lognormal, which is generally a good choice for measurements like these.

In this example, the sample size is small, so the choice of the prior is important. I suspect there is more background information we could use to make a better choice for the prior distribution of sigma.

This example demonstrates the use of grid methods for Bayesian statistics. For many common statistical questions, grid methods like this are simple and fast to compute, especially with libraries like NumPy and SciPy. And they make it possible to answer many useful probabilistic questions.

Data Q&A: Answering the real questions with Python

License: Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International

Destructive Testing

May 7, 2024 AllenDowney

Here’s another installment in Data Q&A: Answering the real questions with Python. Previous installments are available from the Data Q&A landing page.

sample_size

Sample Size Selection¶

Here’s a question from the Reddit statistics forum.

Hi Redditors, I am a civil engineer trying to solve a statistical problem for a current project I have. I have a pavement parking lot 125,000 sf in size. I performed nondestructive testing to render an opinion about the areas experiencing internal delimitation not observable from the surface. Based on preliminary testing, it was determined that 9% of the area is bad, and 11% of the total area I am unsure about (nonconclusive results if bad or good), and 80% of the area is good. I need to verify all areas using destructive testing, I will take out slabs 2 sf in size. my question is how many samples do I need to take from each area to confirm the results with 95% confidence interval?

There are elements of this question that are not clear, and OP did not respond to follow-up questions. But the question is generally about sample size selection, so let’s talk about that.

If the parking lot is 125,000 sf and each sample is 2 sf, we can imagine dividing the total area into 62,500 test patches. Of those, some unknown proportion are good and the rest are bad.

In reality, there is probably some spatial correlation — if a patch is bad, the nearby patches are more likely to be bad. But if we choose a sample of patches entirely at random, we can assume that they are independent. In that case, we can estimate the proportion of patches that are good and quantify the precision of that estimate by computing a confidence interval.

Then we can choose a sample size that meets some requirement. For example, we might want the 95% confidence interval needs to be smaller than a given threshold, or we might want to bound the probability that the proportion falls below some threshold.

But let’s start by estimating proportions and computing confidence intervals.

Click here to run this notebook on Colab.

I’ll download a utilities module with some of my frequently-used functions, and then import the usual libraries.

In [1]:

from os.path import basename, exists

def download(url):
    filename = basename(url)
    if not exists(filename):
        from urllib.request import urlretrieve

        local, _ = urlretrieve(url, filename)
        print("Downloaded " + str(local))
    return filename

download('https://github.com/AllenDowney/DataQnA/raw/main/nb/utils.py')

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns

from utils import decorate

In [2]:

# install the empiricaldist library, if necessary

try:
    import empiricaldist
except ImportError:
    !pip install empiricaldist

The beta-binomial model¶

Based on preliminary testing, it is likely that the proportion of good patches is between 80% and 90%. We can take advantage of that information by using a beta distribution as a prior and updating it with the data. Here’s a prior distribution that seems like a reasonable choice, given the background information.

In [3]:

from scipy.stats import beta as beta_dist

prior = beta_dist(8, 2)
prior.mean()

Out[3]:

0.8

The prior mean is at the low end of the likely range, so the results will be a little conservative. Here’s what the prior looks like.

In [4]:

def plot_dist(dist, **options):
    qs = np.linspace(0, 1, 101)
    ps = dist.pdf(qs)
    ps /= ps.sum()
    plt.plot(qs, ps, **options)

In [5]:

plot_dist(prior, color='gray', label='prior')

decorate(xlabel='Proportion good',
         ylabel='PDF')

This prior leaves open the possibility of values below 80% and greater than 90%, but it assigns them lower probabilities.

Now let’s generate a hypothetical dataset to see what the update looks like. Suppose the actual percentage of good patches is 90%, and we sample n=10 of them.

In [6]:

def generate_data(n, p):
    yes = int(round(n * p))
    no = n - yes
    return yes, no

And suppose that, in line with expectations, 9 out of 10 tests are good.

In [7]:

yes, no = generate_data(n=10, p=0.9)
yes, no

Out[7]:

(9, 1)

Under the beta-binomial model, computing the posterior is easy.

In [8]:

def update(dist, yes, no):
    a, b = dist.args
    return beta_dist(a + yes, b + no)

Here’s how we run the update.

In [9]:

posterior10 = update(prior, yes, no)
posterior10.mean()

Out[9]:

0.85

The posterior mean is 85%, which is half way between the prior mean and the proportion observed in the data.

Here’s what the posterior distribution looks like, compared to the prior.

In [10]:

plot_dist(prior, color='gray', label='prior')
plot_dist(posterior10, label='posterior10')

decorate(xlabel='Proportion good',
         ylabel='PDF')

Given the posterior distribution, we can use ppf, which computes the inverse CDF, to compute a confidence interval.

In [11]:

def confidence_interval(dist, percent=95):
    low = (100 - percent) / 200
    high = 1 - low
    ci = dist.ppf([low, high])
    return ci

Here’s the result for this example.

In [12]:

confidence_interval(posterior10)

Out[12]:

array([0.66862334, 0.96617375])

With a sample size of only 10, the confidence interval is still quite wide — that is, the estimate of the proportion is not precise.

More data?¶

Now let’s run the same analysis with a sample size of n=100.

In [13]:

yes, no = generate_data(n=100, p=0.9)
posterior100 = update(prior, yes, no)
posterior100.mean()

Out[13]:

0.8909090909090909

With a larger sample size, the posterior mean is closer to the proportion observed in the data. And the posterior distribution is narrower, which indicates greater precision.

In [14]:

plot_dist(prior, color='gray', label='prior')
plot_dist(posterior10, label='posterior10')
plot_dist(posterior100, label='posterior100')

decorate(xlabel='Proportion good',
         ylabel='PDF')

The confidence interval is much smaller.

In [15]:

confidence_interval(posterior100)

Out[15]:

array([0.82660267, 0.94180387])

If we need more precision than that, we can increase the sample size more. If we don’t need that much precision, we can decrease it.

With some math, we could compute the sample size algorithmically, but a simple alternative is to run this analysis with different sample sizes until we get the results we need.

But what about that prior?¶

Some people don’t like using Bayesian methods because they think it is more objective to ignore perfectly good background information, even in cases like this where they come from preliminary testing that is clearly applicable.

To satisfy them, we can run the analysis again with a uniform prior, which is not actually more objective, but it seems to make people happy.

In [16]:

uniform_prior = beta_dist(1, 1)
uniform_prior.mean()

Out[16]:

0.5

The mean of the uniform prior is 50%, so it is more pessimistic. Here’s the update with n=10.

In [17]:

yes, no = generate_data(n=10, p=0.9)
uniform_posterior10 = update(uniform_prior, yes, no)
uniform_posterior10.mean()

Out[17]:

0.8333333333333334

Now let’s compare the posterior distributions with the informative prior and the uniform prior.

In [18]:

plot_dist(uniform_prior, color='gray', label='uniform prior')
plot_dist(posterior10, color='C1', label='posterior10')
plot_dist(uniform_posterior10, color='C4', label='uniform posterior10')

decorate(xlabel='Proportion good',
         ylabel='PDF')

With the informative prior, the posterior distribution is a little narrower — an estimate that uses background information is more precise.

Let’s do the same thing with n=100.

In [19]:

uniform_prior = beta_dist(1, 1)
yes, no = generate_data(n=100, p=0.9)
uniform_posterior100 = update(uniform_prior, yes, no)

In [20]:

plot_dist(uniform_prior, color='gray', label='uniform prior')
plot_dist(posterior100, color='C1', label='posterior100')
plot_dist(uniform_posterior100, color='C4', label='uniform posterior100')

decorate(xlabel='Proportion good',
         ylabel='PDF')

With a larger sample size, the choice of the prior has less effect — the posterior distributions are almost the same.

Discussion¶

Sample size analysis is a good thing to do when you are designing experiments, because it requires you to

Make a model of the data-generating process,
Generate hypothetical data, and
Specify ahead of time what analysis you plan to do.

It also gives you a preview of what the results might look like, so you can think about the requirements. If you do these things before running an experiment, you are likely to clarify your thinking, communicate better, and improve the data collection process and analysis.

Sample size analysis can also help you choose a sample size, but most of the time that’s determined by practical considerations, anyway. I mean, how many holes do you think they’ll let you put in that parking lot?

Data Q&A: Answering the real questions with Python

License: Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International

In [ ]:

The mean of a Likert scale?

May 3, 2024 AllenDowney

Here’s another installment in Data Q&A: Answering the real questions with Python. Previous installments are available from the Data Q&A landing page.

likert_mean

Likert scale analysis¶

Here’s a question from the Reddit statistics forum.

I have collected data regarding how individuals feel about a particular program. They reported their feelings on a scale of 1-5, with 1 being Strongly Disagree, 2 being Disagree, 3 being Neutral, 4 being Agree, and 5 being Strongly Agree.

I am looking to analyze the data for averages responses, but I see that a basic mean will not do the trick. I am looking for very simple statistical analysis on the data. Could someone help out regarding what I would do?

It sounds like OP has heard the advice that you should not compute the mean of values on a Likert scale. The Likert scale is ordinal, which means that the values are ordered, but it is not an interval scale, because the distances between successive points are not necessarily equal.

For example, if we imagine that “Neutral” maps to 0 on a number line and “Agree” maps to 1, it’s not clear where we should place “Strongly agree”. And an appropriate mapping might not be symmetric — for example, maybe the people who choose “Strongly agree” are content, but the people who choose “Strongly disagree” are angry. In an arithmetic mean, they would cancel each other out — but that might erase an important distinction.

Nevertheless, I think an absolute prohibition on computing means is too strong. I’ll show some examples where I think it’s a reasonable thing to do — but I’ll also suggest alternatives that might be better.

Click here to run this notebook on Colab.

I’ll download a utilities module with some of my frequently-used functions, and then import the usual libraries.

In [1]:

from os.path import basename, exists

def download(url):
    filename = basename(url)
    if not exists(filename):
        from urllib.request import urlretrieve

        local, _ = urlretrieve(url, filename)
        print("Downloaded " + str(local))
    return filename

download('https://github.com/AllenDowney/DataQnA/raw/main/nb/utils.py')

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns

from utils import decorate

In [2]:

# install the empiricaldist library, if necessary

try:
    import empiricaldist
except ImportError:
    !pip install empiricaldist

Political views¶

As an example, I’ll use data from the General Social Survey (GSS), which I have resampled to correct for stratified sampling.

In [3]:

download('https://github.com/AllenDowney/DataQnA/raw/main/data/gss_qna_extract.hdf')

Out[3]:

'gss_qna_extract.hdf'

In [4]:

gss = pd.read_hdf('gss_qna_extract.hdf', 'gss')

The variable we’ll start with is polviews, which contains responses to this question:

We hear a lot of talk these days about liberals and conservatives. I’m going to show you a seven-point scale on which the political views that people might hold are arranged from extremely liberal–point 1–to extremely conservative–point 7. Where would you place yourself on this scale?

This is not a Likert scale, specifically, but it is ordinal. Here is the distribution of responses:

In [5]:

from utils import values

values(gss['polviews'])

Out[5]:

polviews
1.0     2095
2.0     7309
3.0     7799
4.0    24157
5.0     9816
6.0     9612
7.0     2145
NaN     9457
Name: count, dtype: int64

Here’s the mapping from numerical values to the options that were shown to respondents.

In [6]:

polviews_dict = {
    1: "Extremely liberal",
    2: "Liberal",
    3: "Slightly liberal",
    4: "Moderate",
    5: "Slightly conservative",
    6: "Conservative",
    7: "Extremely conservative",
}

As always, it’s a good idea to visualize the distribution before we compute any summary statistics. I’ll use Pmf from empiricaldist to compute the PMF of the values.

In [7]:

from empiricaldist import Pmf

pmf_polviews = Pmf.from_seq(gss['polviews'])

Here’s what it looks like.

In [8]:

labels = list(polviews_dict.values())
plt.barh(labels, pmf_polviews)
decorate(xlabel='PMF')

The modal value is “Moderate” and the distribution is roughly symmetric, so I think it’s reasonable to compute a mean. For example, suppose we want to know how self-reported political alignment has changed over time. We can compute the mean in each year like this:

In [9]:

mean_series = gss.groupby('year')['polviews'].mean()

And plot it like this.

In [10]:

from utils import plot_series_lowess

plot_series_lowess(mean_series, 'C2')
decorate(xlabel='Year',
         title='Mean political alignment')

I used LOWESS to plot a local regression line, which makes long-term trends easier to see. It looks like the center of mass trended toward conservative from the 1970s into the 1990s and trended toward liberal since then.

When you compute any summary statistic, you lose information. To see what we might be missing, we can use a normalized cross-tabulation to compute the distribution of responses in each year.

In [11]:

xtab = pd.crosstab(gss['year'], gss['polviews'], normalize='index')
xtab.head()

Out[11]:

polviews	1.0	2.0	3.0	4.0	5.0	6.0	7.0
year
1974	0.021908	0.142049	0.149117	0.380212	0.157597	0.127915	0.021201
1975	0.040057	0.131617	0.148069	0.386266	0.145923	0.115880	0.032189
1976	0.021877	0.139732	0.123500	0.398024	0.147495	0.145378	0.023994
1977	0.025085	0.122712	0.145085	0.402712	0.164746	0.111186	0.028475
1978	0.014463	0.096419	0.175620	0.384986	0.182507	0.128788	0.017218

And we can use a heat map to visualize the results.

In [12]:

sns.heatmap(xtab.T, cmap='cividis_r')
plt.gca().invert_yaxis()

Based on the heat map, it seems like the general shape of the distribution has not changed much — so the mean is probably a good way to make comparisons over time.

However, it is hard to interpret the mean in absolute terms. For example, in the most recent data, the mean is about 4.1.

In [13]:

gss.query('year == 2022')['polviews'].mean()

Out[13]:

4.099445902595509

Since 4.0 maps to “Moderate”, we can say that the center of mass is slightly on the conservative side of moderate, but it’s hard to say what a difference of 0.1 means on this scale.

As an alternative, we could add up the percentage who identify as conservative or liberal, with or without an adverb.

In [14]:

con = xtab[[5, 6, 7]].sum(axis=1) * 100
lib = xtab[[1, 2, 3]].sum(axis=1) * 100

And plot those percentages over time.

In [15]:

plot_series_lowess(con, 'C3', label='Conservative')
plot_series_lowess(lib, 'C0', label='Liberal')

decorate(xlabel='Year',
         ylabel='Percent',
         title='Percent identifying as conservative or liberal')

Or we could plot the difference in percentage points.

In [16]:

diff = con - lib
plot_series_lowess(diff, 'C4')

decorate(xlabel='Year',
         ylabel='Percentage points',
         title='Difference %conservative - %liberal')

This figure shows the same trends we saw by plotting the mean, but the y-axis is more interpretable — for example, we could report that, at the peak of the Reagan era, conservatives outnumbered liberals by 10-15 percentage points.

Standard deviation¶

Suppose we are interested in polarization, so we want to see if the spread of the distribution has changed over time. Would it be OK to compute the standard deviation of the responses? As with the mean, my answer is yes and no.

First, let’s see what it looks like.

In [17]:

std_series = gss.groupby('year')['polviews'].std()

In [18]:

plot_series_lowess(std_series, 'C3')
decorate(xlabel='Year',
         ylabel='Standard deviation')

The standard deviation is easy to compute, and it makes it easy to see the long-term trend. If we interpret the spread of the distribution as a measure of polarization, it looks like it has increased in the last 30 years.

But it is not easy to interpret this result in context. If it increased from about 1.35 to 1.5, is that a lot? It’s hard to say.

As an alternative, let’s compute the mean absolute deviation (MAD), which we can think of like this: if we choose two people at random, how much will they differ on this scale, on average?

A quick way to estimate MAD is to draw two samples from the responses and compute the mean pairwise distance.

In [19]:

def sample_mad(series, size=1000):
    data = series.dropna()
    if len(data) == 0:
        return np.nan
    sample1 = np.random.choice(data, size=size, replace=True)
    sample2 = np.random.choice(data, size=size, replace=True)
    mad = np.abs(sample1 - sample2).mean()
    return mad

In [20]:

sample_mad(gss['polviews'])

Out[20]:

1.515

The result is about 1.5 points, which is bigger than the distance from moderate to slightly conservative, and smaller than the distance from moderate to conservative.

Rather than sampling, we can compute MAD deterministically by forming the joint distribution of response pairs and computing the expected value of the distances. For this computation, it is convenient to use NumPy functions for outer product and outer difference.

In [21]:

def outer_mad(series):
    pmf = Pmf.from_seq(series)
    if len(pmf) == 0:
        return np.nan
    ps = np.outer(pmf, pmf)
    qs = np.abs(np.subtract.outer(pmf.index, pmf.index))
    return np.sum(ps * qs)

Again, the result is about 1.5 points.

In [22]:

outer_mad(gss['polviews'])

Out[22]:

1.5360753915376488

Now we can see how this value has changed over time.

In [23]:

mad_series = gss.groupby('year')['polviews'].apply(outer_mad)

Here’s the result, along with the standard deviation.

In [24]:

plt.figure(figsize=(6, 6))
plt.subplot(2, 1, 1)
plot_series_lowess(std_series, 'C3')
decorate(xlabel='',
         ylabel='Standard deviation')

plt.subplot(2, 1, 2)
plot_series_lowess(mad_series, 'C4')

decorate(xlabel='Year',
         ylabel='Mean absolute difference')

The two figures tell the same story — polarization is increasing. But the MAD is easier to interpret. In the 1970s, if you chose two people at random, they would differ by less than 1.5 points on average. Now the difference would be almost 1.7 points. Considering that the difference between a moderate and a conservative is 2 points, it seems like we should still be able to get along.

I think MAD is more interpretable than standard deviation, but it is based on the same assumption that the points on the scale are equally spaced. In most cases, that’s not an assumption we can easily check, but in this example, maybe we can.

For another project, I selected 15 questions in the GSS where conservatives and liberals are most likely to disagree, and used them to estimate the number of conservative responses from each respondent. The following figure shows the average number of conservative responses to the 15 questions for each point on the self-reported scale.

In [25]:

from utils import xticks

conservatism = gss.groupby('polviews')['conservatism'].mean()
conservatism.plot()
xticks(polviews_dict, rotation=30)
decorate(xlabel='Political alignment',
         ylabel='Conservative responses')

The result is close to a straight line, which suggests that the assumption of equal spacing is not bad in this case.

When is the mean bad?¶

In the examples so far, computing the mean and standard deviation of a scale variable is not necessarily the best choice, but it could be a reasonable choice. Now we’ll see an example where it is probably a bad choice.

The variable homosex contains responses to this question:

What about sexual relations between two adults of the same sex–do you think it is always wrong, almost always wrong, wrong only sometimes, or not wrong at all?

If the wording of the question seems loaded, remember that many of the core questions in the GSS were written in the 1970s. Here is the encoding of the responses.

In [26]:

homosex_dict = {
    1: "Always wrong",
    2: "Almost always wrong",
    3: "Sometimes wrong",
    4: "Not wrong at all",
    5: "Other",
}

And here are the value counts.

In [27]:

values(gss['homosex'])

Out[27]:

homosex
1.0    24856
2.0     1857
3.0     2909
4.0    12956
5.0       94
NaN    29718
Name: count, dtype: int64

Before we do anything else, let’s look at the distribution of responses.

In [28]:

pmf_homosex = Pmf.from_seq(gss['homosex'])

In [29]:

labels = list(homosex_dict.values())
plt.barh(labels, pmf_homosex)
decorate(xlabel='PMF')

There are several reasons it’s a bad idea to summarize this distribution by computing the mean. First, one of the responses is not ordered. If we include “Other” in the mean, the result is meaningless.

In [30]:

gss['homosex'].mean()         # total nonsense

Out[30]:

2.099526621672291

If we exclude “Other”, the remaining responses are ordered, but arguably not evenly spaced on a spectrum of opinion.

In [31]:

gss['homosex'].replace(5, np.nan).mean()         # still nonsense

Out[31]:

2.0931232091690544

If we compute a mean and report that the average response is somewhere between “Sometimes wrong” and “Almost always wrong”, that is not an effective summary of the distribution.

The distribution of results is strongly bimodal — most people are either accepting of homosexuality or not. And that suggests a better way to summarize the distribution: we can simply report the fraction of respondents who choose one extreme or the other.

I’ll start by creating a binary variable that is 1 for respondents who chose “Not wrong at all”, 0 for the other responses, and NaN for people who were not asked the question, did not respond, or chose “Other”.

In [32]:

homosex_recode = {
    1: 0,
    2: 0,
    3: 0,
    4: 1,
    5: np.nan,
}

gss['homosex_recode'] = gss['homosex'].replace(homosex_recode)

In [33]:

values(gss['homosex_recode'])

Out[33]:

homosex_recode
0.0    29622
1.0    12956
NaN    29812
Name: count, dtype: int64

The mean of this variable is the fraction of respondents who chose “Not wrong at all”.

In [34]:

gss['homosex_recode'].mean()

Out[34]:

0.30428859974634787

Now we can see how this fraction has changed over time.

In [35]:

percent_series = gss.groupby('year')['homosex_recode'].mean() * 100

In [36]:

plot_series_lowess(percent_series, 'C4')

decorate(xlabel='Year',
         ylabel='Percent',
         title='Percent responding "Not wrong at all"')

The percentage of people who accept homosexuality was almost unchanged in the 1970s and 1980s, and began to increase quickly around 1990. For a discussion of this trend, and similar trends related to racism and sexism, you might be interested in Chapter 11 of Probably Overthinking It.

Discussion¶

Computing the mean of an ordinal variable can be a quick way to make comparisons between groups or show trends over time. The computation implicitly assumes that the points on the scale are equally spaced, which is not true in general, but in many cases it is close enough.

However, even when the mean (or standard deviation) is a reasonable choice, there is often an alternative that is easier to interpret in context.

It’s always good to look at the distribution before choosing a summary statistic. If it’s bimodal, the mean is probably not the best choice.

Data Q&A: Answering the real questions with Python

License: Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International

Appendix: Quantifying discord¶

We’ve seen that mean absolute deviation (MAD) can quantify the average level of disagreement between two people in a population. As a generalization, it can also quantify the discord between two groups.

I might come back and expand this example later.

In [37]:

male = gss.query('sex == 1')
female = gss.query('sex == 2')

pmf_male = Pmf.from_seq(male['polviews'])
pmf_female = Pmf.from_seq(female['polviews'])

In [38]:

labels = list(polviews_dict.values())
plt.barh(labels, pmf_male, height=0.45, align='edge')
plt.barh(labels, pmf_female, height=-0.45, align='edge')
decorate(xlabel='PMF')

In [39]:

ps = np.outer(pmf_male, pmf_female)
qs = np.abs(np.subtract.outer(pmf_male.index, pmf_female.index))
np.sum(ps * qs)

Out[39]:

1.5404976377345188

In [40]:

color_map = {1: 'C0', 2: 'C1'}
sex_dict = {1: 'Male', 2: 'Female'}

for name, group in gss.groupby('sex'):
    series_mean = group.groupby('year')['polviews'].mean()
    plot_series_lowess(series_mean, color_map[name], label=sex_dict[name])
    
decorate(xlabel='Year',
         ylabel='Percentage points',
         title='Mean')

In [41]:

def compute_diff(df):
    xtab = pd.crosstab(df['year'], df['polviews'], normalize='index')
    lib = xtab[[1, 2, 3]].sum(axis=1) * 100
    con = xtab[[5, 6, 7]].sum(axis=1) * 100
    return con - lib

In [42]:

color_map = {1: 'C0', 2: 'C1'}
sex_dict = {1: 'Male', 2: 'Female'}

for name, group in gss.groupby('sex'):
    diff = compute_diff(group)
    plot_series_lowess(diff, color_map[name], label=sex_dict[name])
    
decorate(xlabel='Year',
         ylabel='Percentage points',
         title='Difference %conservative - %liberal')

	score	frequency	cumulative frequency	cumulative percentage
0	8	1	1	2
1	9	1	2	4
2	10	1	3	6
3	11	3	6	13
4	12	5	11	23
5	13	7	18	38
6	14	8	26	54
7	15	9	35	73
8	16	6	41	85
9	17	4	45	94
10	18	2	47	98
11	19	1	48	100

	score	frequency	cumulative frequency	cumulative percentage
0	8	1	1	2
1	9	1	2	4
2	10	1	3	6
3	11	3	6	13
4	12	5	11	23
5	13	7	18	38
6	14	8	26	54
7	15	9	35	73
8	16	6	41	85
9	17	4	45	94
10	18	2	47	98
11	19	1	48	100

	score	frequency	cumulative frequency	cumulative percentage
0	8	1	1	2
1	9	1	2	4
2	10	1	3	6
3	11	3	6	13
4	12	5	11	23
5	13	7	18	38
6	14	8	26	54
7	15	9	35	73
8	16	6	41	85
9	17	4	45	94
10	18	2	47	98
11	19	1	48	100