COVID-19 and the Inspection Paradox
The inspection paradox (aka length-biased sampling) is one of my favorite topics, and it turns out to be useful in the fight against COVID-19.
During the pandemic, you have probably heard about about the effective reproduction number, R, which is the average number of people infected by each infected person. R is important because it determines the large-scale course of the epidemic. As long as R is greater than 1, the number of cases will grow exponentially; if we find ways to drive R below 1, the number of cases will dwindle toward zero.
However, R is an average, and the average is not the whole story. With COVID-19, like many other epidemics, there is a lot of variation around the average.
According to a news feature in Nature, “One study in Hong Kong found that 19% of cases of COVID-19 were responsible for 80% of transmission, and 69% of cases didn’t transmit the virus to anyone.” In other words, most infections are caused by a small number of superspreaders.
This observation suggests a strategy for contact tracing. When an infected patient is discovered, it is common practice to identify people they have been in contact with who might also be infected. “Forward tracing” is intended to find people the patient might have infected; “backward tracing” is intended to find the person who infected the patient.
Now suppose you are a public health officer trying to slow or stop the spread of a communicable disease. Assuming that you have limited resources to trace contacts and test for the disease — and that’s a pretty good assumption — which do you think would be more effective, forward or backward tracing?
The inspection paradox suggests that backward tracing is more likely to discover a superspreader and the people they have infected.
According to the Nature article, “[Backward tracing] is extremely effective for the coronavirus because of its propensity to be passed on in superspreading events […] Any new case is more likely to have emerged from a cluster of infections than from one individual, so there’s value in going backwards to find out who else was linked to that cluster.”
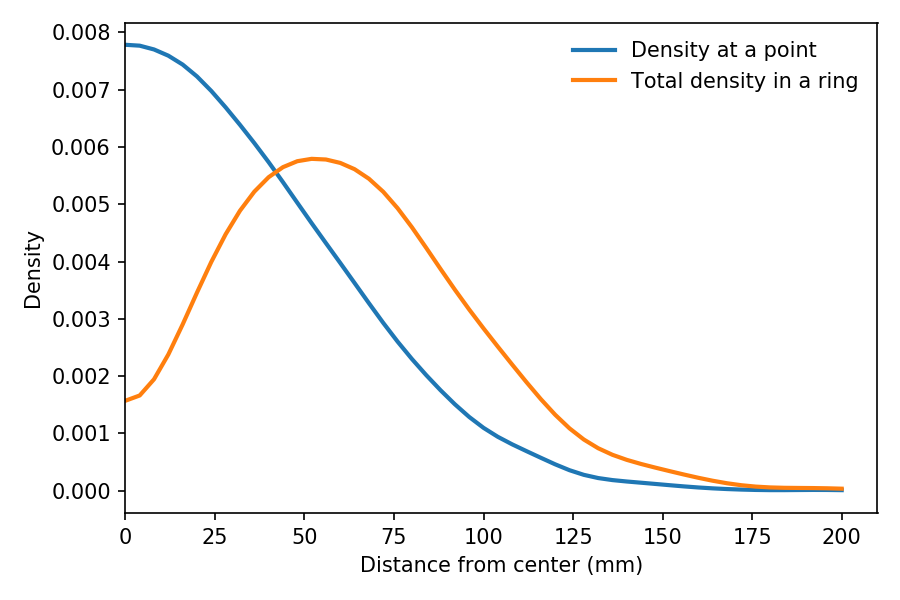
To quantify this effect, let’s suppose that 70% of infected people don’t infect anyone else, as in the Hong Kong study, and the other 30% infect between 1 and 15 other people, uniformly distributed. The average of this distribution is 2.4, which is a plausible value of R.
Now suppose we discover an infected patient, trace forward, and find someone the patient infected. On average, we expect this person to infect 2.4 other people.
But if we trace backward and find the person who infected the patient, we are more likely to find someone who has infected a lot of people, and less likely to find someone who has only infected a few. In fact, the probability that we find any particular spreader is proportional to the number of people they have infected.
By simulating this sampling process, we can compute the distribution we would see by backward tracing. The average of this biased distribution is 10.1, more than four times the average of the unbiased distribution. This result suggests that backward tracing can discover four times more cases than forward tracing, given the same resources.
This example is not just theoretical; Japan adopted this strategy in February 2020. As Michael Lewis describes in The Premonition:
“When the Japanese health authorities found a new case, they did not waste their energy asking the infected person for a list of contacts over the previous few days, to determine whom the person might have infected in turn. […] Instead, they asked for a list of people with whom the infected person had interacted with further back in time. Find the person who had infected the newly infected person and you might have found a superspreader. Find a superspreader and you could track down the next superspreader before [they] really got going.”
So the inspection paradox is not always a nuisance; sometimes we can use it to our advantage.
This article is an excerpt from a new book I am working on, Probably Overthinking It: The puzzles and paradoxes of probability.