One of the exercises in Modeling and Simulation in Python invites readers to download estimates of world population from 10,000 BCE to the present, and to see if they are well modeled by any simple mathematical function. Here’s what the estimates look like (aggregated on Wikipedia from several researchers and organizations):

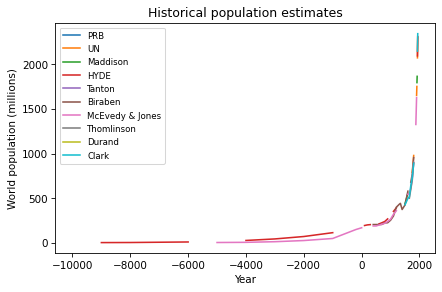
After some trial and error, I found a simple model that fits the data well: a / (b-x), where a is 300,000 and b is 2100. Here’s what the model looks like compared to the data:

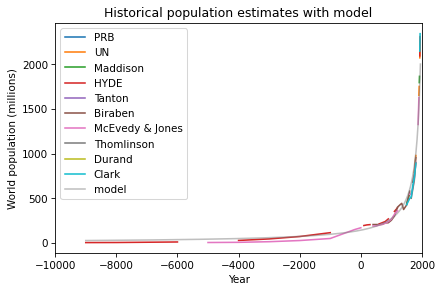
So that’s a pretty good fit, but it’s a very strange model. The first problem is that there is no theoretical reason to expect world population to follow this model, and I can’t find any prior work where researchers in this area have proposed a model like this.

The second problem is that this model is headed for a singularity: it goes to infinity in 2100. Now, there’s no cause for concern — this data only goes up to 1950, and as we saw in this previous article, the nature of population growth since then has changed entirely. Since 1950, world population has grown only linearly, and it is now expected to slow down and stop growing before 2100. So the singularity has been averted.

But what should we make of this strange model? We can get a clearer view by plotting the y-axis on a log scale:

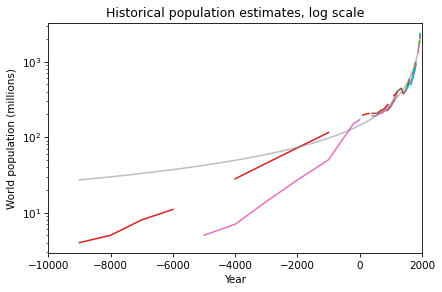
On this scale, we can see that the model does not fit the data as well prior to 4000 BCE. I’m not sure how much of a problem that is, considering that the estimates during that period are not precise. The retrodictions of the model might actually fall within the uncertainty of the estimates.

Regardless, even if the model only fits the data after 4000 BCE, it is still worth asking why it fits as well as it does. One step toward an answer is to express the model in terms of doubling time. With a little math, we can show that a function with the form a / (b-x) has a doubling time that decreases linearly.

In 10,000 BCE, doubling time was about 8000 years, in 5000 BCE, it was about 5000 years, and in Year 0, it was 1455 years. Doubling time decreased because of the Neolithic Revolution, which was the transition of human populations from hunting and gathering to agriculture and settlement, starting about 10,000 years ago.

During this period, the domestication of plants and animals vastly increased the calories people could obtain, and the organization of large, permanent settlements accelerated the conversion of those calories into population growth.

If we zoom in on the last 2000 years, we see that the most recent data points are higher and steeper than the model’s predictions, which suggest that the Industrial Revolution accelerated growth even more.

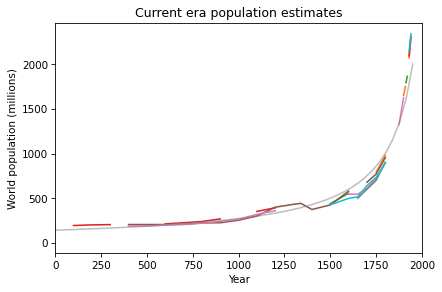
So, if the Neolithic Revolution started world population on the path to a singularity, and the Industrial Revolution sped up the process, what stopped it? Why has population growth since 1950 slowed so dramatically?

The ironic answer is the Green Revolution, which increased our ability to produce calories so quickly, it contributed to rapid improvements in public health, education, and economic opportunity — all of which led to drastic decreases in child mortality. And, it turns out, when children are likely to survive, people choose to have fewer of them.

As a result, population growth left the regime where doubling time decreases linearly, and entered a regime where doubling time increases linearly. And soon, if not already, it will enter a regime of deceleration and decline. At this point it is unlikely that world population will ever double again.

So, to summarize the last 10,000 years of population growth, the Neolithic and Industrial Revolutions made it possible for humans to breed like crazy, and the Green Revolution made it so we don’t want to.

This article is based on an exercise in Modeling and Simulation in Python, now available from No Starch Press and Amazon.com. You can download the data and run the code in this Jupyter notebook.