I have published the first five chapters of Think Linear Algebra! You can read them here or follow these links to run the notebooks on Colab. Here are the chapters I have so far:

Chapter 1: The Power of Linear Algebra
Introduces matrix multiplication and eigenvectors through a network-based model of museum traffic, and implements the PageRank algorithm for quantifying the quality of web pages.

Chapter 5: To Boldly Go
Uses matrices scale, rotate, shear, and translate vectors. Applies these methods to 2D compute graphics, including a reimplementation of the classic video game Asteroids.

Chapter 7: Systems of Equations
Applies LU decomposition and matrix equations to analyze electrical circuits. Shows how linear algebra solves real engineering problems.

Chapter 8: Null Space
Investigates chemical stoichiometry as a system with multiple valid solutions. Introduces concepts of rank and nullspace to describe the solution space.

Chapter 9: Truss the System
Models structural systems where the unknowns are vector forces. Uses block matrices and rank analysis to compute internal stresses in trusses.

As you can tell by the chapter numbers, there is more to come — although the sequence of topics might change.

If you are curious about this project, here’s more about why I’m writing this book.

Math is not real

In this previous article, I wrote about “math supremacy”, which is the idea that math notation is the real thing, and everything else — including and especially code — is an inferior imitation.

I am confronted with math supremacy more often than most people, because I write books that use code to present ideas that are usually expressed in math notation. I think code can be simpler and clearer, but not everyone agrees, and some of them disagree loudly.

With Think Linear Algebra, I am taking my “code first” approach deep into the domain of math supremacy. Today I was using block matrices to analyze a truss, an example I remember seeing in my college linear algebra class. I remember that I did not find the example particularly compelling, because after setting up the problem — and it takes a lot of setting up — we never really finished it. That is, we talked about how to analyze a truss, hypothetically, but we never actually did it.

This is a fundamental problem with the way math is taught in engineering and the sciences. We send students off to the math department to take calculus and linear algebra, we hope they will be able to apply it to classes in their major, and we are disappointed — and endlessly surprised — when they can’t.

Part of the problem is that transfer of learning is much harder than many people realize, and does not happen automatically, as many teachers expect.

Another part of the problem is what I wrote about in Modeling and Simulation in Python: a complete modeling process involves abstraction, analysis, and validation. In most classes we only teach analysis, neglecting the other steps, and in some math classes we don’t even do that — we set up the tools to do analysis and never actually do it.

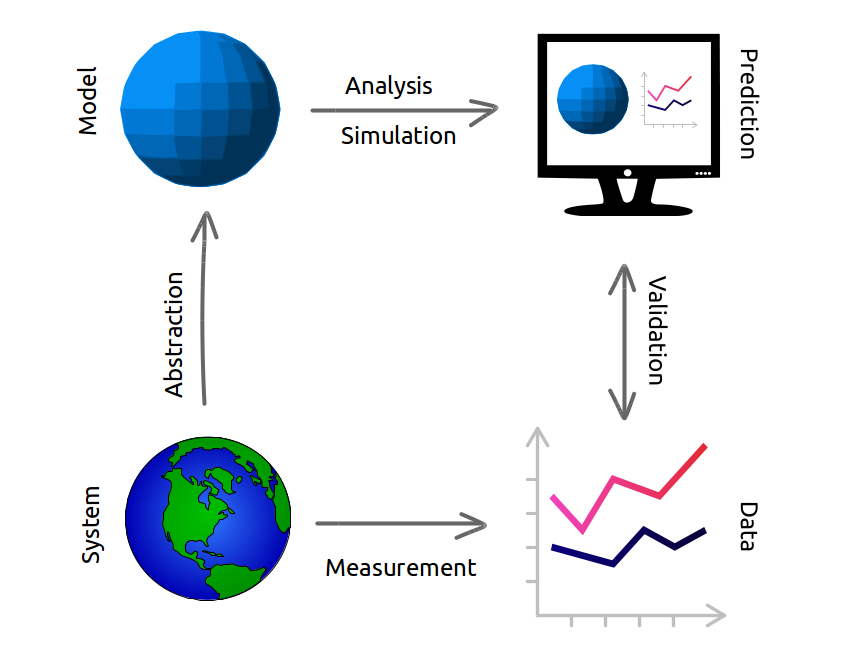
This is the power of the computational approach — we can demonstrate all of the steps, and actually solve the problem. So I find it ironic when people dismiss computation and ask for the “math behind it”, as if theory is reality and reality is a pale imitation. Math is a powerful tool for analysis, but to solve real problems, it is not the only tool we need. And it is not, contrary to Plato, more real than reality.