I have mixed feelings about Bayesian hypothesis testing. On the positive side, it’s better than null-hypothesis significance testing (NHST).

And it is probably necessary as an onboarding tool: Hypothesis testing is one of the first things future Bayesians ask about; we need to have an answer.

On the negative side, Bayesian hypothesis testing is often unsatisfying because the question it answers is not the most useful question to ask.

To explain, I’ll use an example from Bite Size Bayes, which is a series of Jupyter notebooks I am writing to introduce Bayesian statistics.

In Notebook 7, I present the following problem from David MacKay’s book, Information Theory, Inference, and Learning Algorithms:

“A statistical statement appeared in The Guardian on Friday January 4, 2002:

“When spun on edge 250 times, a Belgian one-euro coin came up heads 140 times and tails 110. ‘It looks very suspicious to me’, said Barry Blight, a statistics lecturer at the London School of Economics. ‘If the coin were unbiased the chance of getting a result as extreme as that would be less than 7%’.”

“But [asks MacKay] do these data give evidence that the coin is biased rather than fair?”

I start by formulating the question as an estimation problem. That is, I assume that the coin has some probability, x, of landing heads, and I use the data to estimate it.

If we assume that the prior distribution is uniform, which means that any value between 0 and 1 is equally likely, the posterior distribution looks like this:

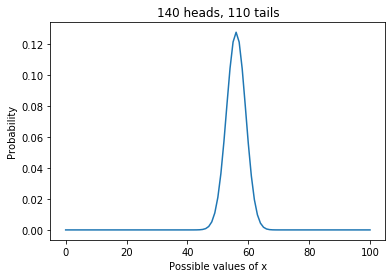
This distribution represents everything we know about x given the prior and the data. And we can use it to answer whatever questions we have about the coin.

So let’s answer MacKay’s question: “Do these data give evidence that the coin is biased rather than fair?”

The question implies that we should consider two hypotheses:

• The coin is fair.
• The coin is biased.

In classical hypothesis testing, we would define a null hypothesis, choose a test statistic, and compute a p-value. That’s what the statistician quoted in The Guardian did. His null hypothesis is that the coin is fair. The test statistic is the difference between the observed number of heads (140) and the expected number under the null hypothesis (125). The p-value he computes is 7%, which he describes as “suspicious”.

In Bayesian hypothesis testing, we choose prior probabilities that represent our degree of belief in the two hypotheses. Then we compute the likelihood of the data under each hypothesis. The details are in Bite Size Bayes Notebook 12.

In this example the answer depends on how we define the hypothesis that the coin is biased:

• If you know ahead of time that the probability of heads is exactly 56%, which is the fraction of heads in the dataset, the data are evidence in favor of the biased hypothesis.
• If you don’t know the probability of heads, but you think any value between 0 and 1 is equally likely, the data are evidence in favor of the fair hypothesis.
• And if you have knowledge about biased coins that informs your beliefs about x, the data might support the fair or biased hypothesis.

In the notebook I summarize these results using Bayes factors, which quantify the strength of the evidence. If you insist on doing Bayesian hypothesis testing, reporting a Bayes factor is probably a good choice.

But in most cases I think you’ll find that the answer is not very satisfying. As in this example, the answer is often “it depends”. But even when the hypotheses are well defined, a Bayes factor is generally less useful than a posterior distribution, because it contains less information.

The posterior distribution incorporates everything we know about the coin; we can use it to compute whatever summary statistics we like and to inform decision-making processes. We’ll see examples in the next two notebooks.